Problem Statement:

A professional cyclist is cycling at 13 m/s in a race.

1. Neglecting rolling resistance, how much power must the cyclist expend to race at this speed? Assume the density of air is 1.20 kg/m³.
2. If the cyclist switches to a bicycle enclosed in a streamlined faring, how much faster will she be able to go?

Solution:

(a) If rolling resistance is ignored, the force supplied by the cyclist is used to overcome drag alone and these two forces balance. Thus, the power expended can be computed as

Using the C_D and A values from the drag coefficient table we have

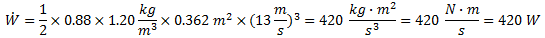
That is about 0.56 hp. Note we have converted 3.9 ft² to 0.362 m² for A (1 ft = 0.3048 m).

(b) If it is the same cyclist, we can assume the power output is the same as in part (a), but now the drag coefficient and cross-sectional area are different. From the drag coefficient table we find C_D = 0.12 and A = 5.0 ft² = 0.465 m². Using the relationship between 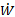and V₀ from part (a) we have

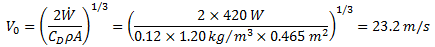
which is about 52 mph.