Chapter 2 Computation of Material Composition and Band Edges

This chapter includes the introduction of the input parameters for each material system and the output files generated by running the material system. The given example is for 1.55um single quantum well strain compensated SCH structure. For a better reading of this manual, the following conventions are used for giving the example of running the program. The Italic style is for the output screen from the screen of the program. The user’s typing starts with a “>” to indicate the user’s input.

2.1 Input Parameters for Each Material System

There are four major kinds of input parameters (I, II, III, and IV) for each material system. The following paragraph explains each input parameters:

I) # For GRIN STRUCTURE (STEP) N=:

This is the number of the layers except for the quantum well. For example, the simple SCH quantum well structure has the “N” which equals to 2. For the graded index SCH structure with single quantum well that can have 10 steps between the quantum part and cladding part, we then need to give N equaling to 11. N-1 does not include the cladding layer. Figure 2.1.1 shows the different conduction band structure of the simple and graded index SCH.

Figure 2.1.1 Different SCH structure for band edge profile

II) WELL, BARRIER AND CLADDING WAVELENGTH:

The wavelength range differs with the material system. We give the wavelength range for each material system layer in appendix A. The QW wavelength has the highest wavelength, then barrier wavelength and then cladding because of the band gap difference for different layers. The wavelength in the QW is related to the desired lasing wavelength. However, the input wavelength is approximated according to the bulk material’s energy band gap. If the user know the composition for quantum well, barrier and cladding layer, the appendix A provides the formula to calculate the wavelength. The wavelength in um can be obtained from 1.24/energy band gap.

III) CLADDING, BARRIER, and QUANTUM WELL WIDTH:

Users can input the desired width value in am-strong Å. If the GRINSCH and multiple quantum wells structure is for the desired structure, the user needs to be aware of the input value for the barrier width. The program divides the input barrier width over N-1 as the barrier width between the quantum wells.

IV) INPUT STRAIN:

From the strain constant (e) [1],

(2.1)

where a_q , a_b are lattice constants of the quantum well and barrier layers, respectively. From energy band semiconductor structure, figure 2.1.2, we know that the value of tensile strain is positive for a_q< a_b, and compressive strain has a negative value for a_q> a_b. (2.1) is good for the unstrained barrier and the barrier is lattice matched to the substrate. In (2.1), we can always put a_q as the strain layer and a_b for unstrain layer, which is usually lattice match to the substrate, to calculate the strain. For example, if we put strain in the barrier, we will have the barrier lattice as a_q and substrate lattice as a_b.

The other definition is often used for the strain constant

(2.2)

where a_u is the unstrained layer and usually lattice match to substrate, a_s is the strained layer

For this definition, a_s > a_u is compressive strain. We will get the positive strain constant. Similarly, if a_s < a_u, which is tensile strain, we will get the negative strain constant. However, for the Gain program, we use the equation (2.1) for the definition of the strain constant.

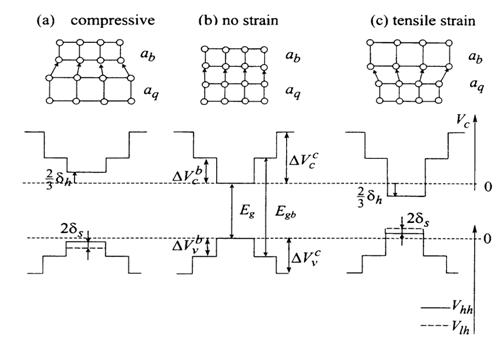
Figure 2.2.2 Energy band semiconductor structure. The conduction V_c and valence V_hh, V_lh potentials for a semiconductor structure with quantum-well, barrier and cladding layers. Notation: d_h: hydrostatic potential, d_s:shear potential, E_g: energy band gap for quantum well, E_gb: energy band gap for barrier, DV_c^b: conduction band offsets for the barrier, DV_c^c: conduction band offsets for the cladding, DV_v^b: valence band offsets for the barrier, DV_v^c: valence band offsets for the cladding.

Different material systems may have slightly different input parameters and procedures. The only big variation is for material system #10, which does not need the wavelength and width input parameters. So a list of input parameters and steps for each material system is shown in Table 2.1 based on the order that they appear in program screen.

Table 2.1 Necessary input steps for each material system

Material	Step 1	Step 2	Step 3	Step 4
(1)AlGaAs/AlGaAs	# of GRIN	QW wavelength	Barrier wavelength	Cladding wavelength
(2)InGaAsP/InGaAs	# of GRIN	QW wavelength	Barrier wavelength	Cladding wavelength
(3)InGaAs/InGaAsP/InP	# of GRIN	QW wavelength	Barrier wavelength	Cladding wavelength
(4)InGaAlAs/InGaAlAs	# of GRIN	QW wavelength	Barrier wavelength	Cladding wavelength
(5)GaInP/(AlGa)0.5In0.5P/AlInP	# of GRIN	QW wavelength	Barrier wavelength	Cladding wavelength
(6)InGaAs/AlGaAs/AlGaAs	# of GRIN	QW wavelength	Barrier wavelength	Cladding wavelength
(7)InGaAs/InGaAsP/Ga0.51In0.49P(MATCHED GaAs)	# of GRIN	QW wavelength	Barrier wavelength	Cladding wavelength
(8)AlyInxGa1-x-yAs/AlzGa1-zAs/GaAs	# of GRIN	QW wavelength	Barrier wavelength	Cladding wavelength
(9)InzGa1-zAs/AlxGayIn1-x-yAs/InP	# of GRIN	QW wavelength	Barrier wavelength	Cladding wavelength
(10)InGaAlAs/InGaAlAs/AlAsxSb1-x(matched InP)	Compress or Tensile	J	Strain
(11)InzGa1-zAs/AlxGayIn1-x-yAs/AlAsxSb1-x	# of GRIN	QW wavelength	Barrier wavelength	Cladding wavelength
(12)In(y)Ga(1-y)As(x)N(1-x)/GaAs (dilute N)	# of GRIN	QW wavelength	Barrier wavelength	Cladding wavelength
(13)In(1-x)Ga(x)As(y)P(1-y)/GaAs	# of GRIN	QW wavelength	Barrier wavelength	Cladding wavelength

Table 2.1 Necessary input steps for each material system (continued)

Material	Step 5	Step 6		Step 7
(1)AlGaAs/AlGaAs	Input C, B, QW width in Å
(2)InGaAsP/InGaAs	Input C, B, QW width in Å	Input Ex		Lattice matched barrier
				Strain compensated(then input strain Ex for barrier)
(3)InGaAs/InGaAsP/InP	Input C, B, QW width in Å	Lattice matched barrier
		Strain compensated		Input strain Ex for barrier
(4)InGaAlAs/InGaAlAs	Input C, B, QW width in Å	Input strain	Choose Dr.Chuang or experimental			Lattice match
						Input strain		Choose (1) or (2)
(5)GaInP/(AlGa)0.5In0.5P/AlInP	Input C, B, QW width in Å	AlGaInP lattice match to GaAs
		AlGaInP mismatch			Input strain
(6)InGaAs/AlGaAs/AlGaAs	Input C, B, QW width in Å
(7)InGaAs/InGaAsP/Ga0.51In0.49P(MATCHED GaAs)	Input C, B, QW width in Å	Input wavelength for barrier
(8)AlyInxGa1-x-yAs/AlzGa1-zAs/GaAs	Input C, B, QW width in Å	Input strain
(9)InzGa1-zAs/AlxGayIn1-x-yAs/InP	Input C, B, QW width in Å	Lattice matched barrier
		Strain compensated			Dr.Chuang’s		Input strain
					Experimental
(10)InGaAlAs/InGaAlAs/AlAsxSb1-x(matched InP)
(11)InzGa1-zAs/AlxGayIn1-x-yAs/AlAsxSb1-x	Input C, B, QW width in Å
(12)In(y)Ga(1-y)As(x)N(1-x)/GaAs (dilute N)	Input C, B, QW width in Å	Input strain
(13)In(1-x)Ga(x)As(y)P(1-y)/GaAs	Input C, B, QW width in Å	Lattice matched barrier
		Strain compensated			Input strain EX

2.2 Output Parameters

Two output files – CBANDEG.DAT and VBANDEG.DAT will be generated after running the step of “FOR THE NECESSARY PARAMETERS” in GAIN program by inputting all the necessary parameters for the selected material system. In both files, the first row contains the strain and lattice constant of quantum well, the 1^st, 2^nd and 3^rd column of the rest rows show the layer thickness, composition of x component, and composition of y component for each layer, respectively. The 4^th column of CBANDEG.DAT gives conduction band offset for each layer while that of VBANDEG.DAT gives valance band offset for each layer.

The unit of layer thickness and lattice constant in both CBANDEG.DAT and VBANDEG.DAT is angstrom, and the unit of energy band offsets is electron volts (eV). The compressive-strained quantum well has a negative value of strain as opposed to the positive strain value of tensile-strained quantum well. The zero energy reference level for conduction band offset is non-strained quantum well bulk material conduction band edge, and the zero energy reference level for valance band offset is non-strained quantum well bulk material valance band edge. Therefore, as indicated by Figure 2.1.2, the quantum well conduction band offset is zero for non-strained quantum well, positive for compressive-strained quantum well and negative for tensile-strained quantum well. Vise versa for the valance band offset of the quantum well. The barrier and cladding band offsets are always positive for conduction band and negative for valance band.

If we use QW, BR, CL as acronyms of quantum, barrier and cladding, and assume that the material components for each layer has the general form of A(x)B(1-x)C(y)D(1-y) with A,B,C,D represent the arbitrary 4 material elements and x, 1-x, y, 1-y represent the compositions of A, B, C and D, use 5-layer symmetric structure as an example, the CBANDEG.DAT and VBANDEG.DAT have the general forms as shown below.

CBANDEG.DAT (conduction band structure)

QW_strain QW_lattice constant

CL thickness CL x-composition CL y-composition CL C-band offset

BR thickness BR x-composition BR y-composition BR C-band offset

QW thickness QW x-composition QW y-composition QW C-band offset

BR thickness BR x-composition BR y-composition BR C-band offset

CL thickness CL x-composition CL y-composition CL C-band offset

VBANDEG.DAT (valence band str ucture)

QW_strain QW_lattice constant

CL thickness CL x-composition CL y-composition CL V-band offset

BR thickness BR x-composition BR y-composition CR V-band offset

QW thickness QW x-composition QW y-composition QW V-band offset

BR thickness BR x-composition BR y-composition BR V-band offset

CL thickness CL x-composition CL y-composition CL V-band offset

2.3 Running the Software for Material Composition and Band Edge Calculations

In this section, we show the details of how to run the GAIN program to calculate the material compositions and band edges. As shown in section 2.2, the output files, “cbandeg.dat” and “vbandeg.dat”, give the band gap, composition and layer thickness information.

2.3.1 Selecting the Material System

After typing “GAINV1A” under the executable file directory from the DOS prompt or directly double click on the gain program executable file, the program will prompt the following:

****************************************************

THE MAIN PROGRAM IS ONLY A CALLING PROGRAM, WHICH

CONTAINS THREE MAJOR PARTS (MORE THAN 20 SUBROUTINES

FIRST SELECT MATERIAL PARAMETERS.

SECOND SELECT ENERGY LEVELS IN BOTH BANDS.

THIRD FIND THE G(J), G(WAVELENGTH) AND RATE EQUATIONS

****************************************************

MAKE YOUR SELECTION NOW!

ENTER 1 FOR THE NECESSARY PARAMETERS

2 FOR THE ENERGY VALUES OF CONDUCTION BAND

3 FOR THE ENERGY VALUES OF HEAVY HOLE BAND

4 FOR THE ENERGY VALUES OF LIGHT HOLE BAND

5 FOR THE LASER G-J AND G(LAMBDA)

6 FOR RATE EQUATIONS(TWO SECTION MODEL INCLUDED)

7 FOR EXIT

q Note: The program is asking the user what to calculate. As a start, we entered 1 to calculate the necessary parameters to calculate the material compositions and band edges.

ENTER 1 FOR AlGaAs/AlGaAs

2 FOR InGaAsP/InGaAsP/InP

3 FOR InGaAs/InGaAsP/InP

4 FOR InGaAlAs/InGaAlAs/InP

5 FOR GaInP/(AlGa)0.5In0.5P/AlInP

6 FOR InGaAs/AlGaAs/AlGaAs

7 FOR InGaAs/InGaAsP/Ga0.51In0.49P(MATCHED GaAs)

8 FOR AlyInxGa1-x-yAs/AlzGa1-zAs/GaAs

9 FOR InzGa1-zAs/AlyGaxIn1-x-yAs/InP

10 FOR InGaAlAs/InGaAlAs/AlAsxSb1-x(matched InP)

11 FOR InzGa1-zAs/AlyGaxIn1-x-yAs/AlAsxSb1-x

12 FOR In(y)Ga(1-y)As(x)N(1-x)/GaAs (dilute N)

13 FOR In(1-x)Ga(x)As(y)P(1-y)/GaAs

14 FOR EXIT, BACK TO MAIN PAGE!

q Note: Here we chose material system 4 as an example of running the GAIN program in this manual.

INPUT THE LAYER # FOR GRIN STRUCTURE(STEP)

STEP N=

q Note: For this five layers structure, which include one quantum well, two barriers and two cladding layers, we enter 2 steps which include one barrier and one cladding as the total number of GRIN structure.

INPUT THE WELL WAVELENGTH (um)

>1.813385122

q Note: If you know your material composition, you can refer to appendix A to calculate the desired wavelength for the quantum well. Otherwise, you can use the initial guess value that is close to your desired wavelength.

INPUT THE BARRIER WAVELENGTH (um)

>1.023516108

q Note: If you know your material composition, you can refer to appendix A to calculate the desired wavelength for the barrier. Otherwise, you can use the initial guess value.

INPUT THE CLADDING WAVELENGTH (um)

>0.828002068

q Note: If you know your material composition, you can use appendix A to calculate the desired wavelength for the quantum cladding. Otherwise, you can use the initial guess value.

BANDGAP ENERGY OF QUANTUM WELL= 0.683804000019804 eV

INPUT CLADDING, BARRIER,QUANTUM WELL WIDTH (A)

>100 50 60

q Note: Input the desired values in the unit of angstrom.

FOR AlyGaxIn(1-x-y)As, in output read Ga first then Al

IF ONE OF THE COMPONENTS IN ACTIVE REGION IS ZERO,

YOU HAVE TO TRY ANOTHER INITIAL GUESS FOR

BOTH WAVELENGTH AND STRAIN

INPUT STRAIN

>-0.011704948

q Note: This is a compressive strain for quantum well.

FOR Eg relation from Dr. Chuang,s book input 1,

for Industrial experimental formula input 2

INPUT =--> ?

q Note: Please refer to appendix A for the different formula.

FOR BARRIER IS LATTICE MATCHED SELECT ==>1

FOR BARRIER IS STRAIN COMPENSATED SELECT ==> 2

SELECTION IS ===> ?

q Note: For this example, we have the strain compensate.

FOR Eg relation from Dr. Chuang,s book input 1,

for Industrial experimental formula input 2

INPUT =--> ?

q Note: See appendix A.

INPUT STRAIN==>?

>0.008776922

q Note: Input the barrier strain. In this example, we have the tensile strain.

WRITE CONDUCTION BAND PARAMETERS INTO CBANDEG.DAT

WRITE VALENCE BAND PARAMETERS INTO VBANDEG.DAT

INPUT 1 FOR NEW CALCULATION

2 FOR EXIT

INPUT =?

q Note: Finish the band edge calculation.

2.3.2 Band edge out put files

After we running the above steps, we will have two output files. “cbandeg.dat” has the information about the conduction band. “vbandeg.dat” includes the valence band information.

The following is the content of the “cbandeg.dat”

-.117049E-01 0.593758E-09

0.10000000E+03 0.00000000E+00 0.4829333 0.5859193

0.50000000E+02 0.34879557E+00 0.2505339 0.3327401

0.60000000E+02 0.21964924E+00 0.0801355 0.0538058

0.50000000E+02 0.34879557E+00 0.2505339 0.3327401

0.10000000E+03 0.00000000E+00 0.4829333 0.5859193

The following is for the “vbandeg.dat”:

-.117049E-01 0.593758E-09

0.10000000E+03 0.00000000E+00 0.4829333 -0.2278575

0.50000000E+02 0.34879557E+00 0.2505339 -0.1241536

0.60000000E+02 0.21964924E+00 0.0801355 -0.0269029

0.50000000E+02 0.34879557E+00 0.2505339 -0.1241536

0.10000000E+03 0.00000000E+00 0.4829333 -0.2278575

As for the examples of different structures, please refer to the appendix A.

Chapter 3 Energy Band Calculations

A brief introduction about calculation of the energy values will be given in section 3.1. In section 3.2, the input and output parameters of the program will be explained. In section 3.3, the input and output files will be discussed. Finally in section 3.4, the energy values for conduction and valence (heavy hole and light hole) bands will be calculated for a specific material system as an example by running the steps of the program.

3.1 Brief Overview for Energy Band Calculations

When the thickness of the active region, which can be any low-energy gap semiconductor layer confined between higher-energy gap semiconductors, becomes comparable to the de Broglie wavelength (l ≈ h / p), quantum mechanical effects are expected to occur. These effects are observed in the absorption and emission characteristics in the lasers.

A carrier (electron or hole) in a double heterostructure is confined within a three-dimensional potential well. The energy levels of such carriers are obtained by separating the system Hamiltonian into the three parts, corresponding to the kinetic energies in the x, y, and z directions. When the thickness of the heterostructure (L_z, see Fig. 3.1.1) is comparable to the de Broglie wavelength, the kinetic energy corresponding to the carrier motion along the z direction is quantized. The energy levels form a continuum of states given by

(3.1)

where k_x and k_y are the wave vector components along the x and y directions and m is the effective mass of the carrier respectively.

From the equation above, the energy levels in the z direction are obtained by solving the Shröd inger equation for a one-dimensional potential well given by

inside the well (3.2)

outside the well (3.3)

For a finite well, the energy levels and wave functions can be obtained from Eq. (3.2) by using the boundary conditions that y and dy/dz are continuous at the interfaces z = 0 and z = L_z, The solution is

(3.4)

where

(3.5)

The quantities A, B, C and δ are constants. Using the boundary conditions stated above, the following eigenvalue equation is obtained;

(3.6)

This eigenvalue equation is numerically solved to yield the energy levels E_n of a particle in a potential well.

Taking into account discrete states along the z direction and continuous states along the x and y directions, the energy eigenvalues for a particle confined in the quantum well are

(3.7)

where E_n is the nth confined-particle energy level for carrier motion and to the well and

is the effective mass for this level.

Fig. 3.1.1 Schematic representation of the confined particle energy levels of electrons, heavy holes and light holes in a quantum well.

Figure 3.1.1 shows schematically the energy levels E_n of electrons and holes confined within a quantum well. The confined-particle energy levels E_n are denoted by E_1C, E_2C, E_3C for electrons; E_1hh, E_2hh, and E_3hh for heavy holes; and E_1lh, E_2lh, and E_2lh for light holes. These quantities can be calculated by solving the eigenvalue equation (3.6) for a given potential barrier (∆E_C or ∆E_V).

For the multilayer structure including quantum wells, barrier and cladding layers, the energy eigenvalue equation is obtained using Transfer Matrix Method (TMM) approach by matching the field values and their first order derivatives at each boundary. The clear and detailed discussion about TMM can be found in [7].

3.2 Explanations on Input and Output Parameters

This section provides a detailed explanation for the input and output parameters that appears in section 3.4. These parameters are necessary to calculate the energy levels in the conduction and valence bands.

3.2.1 Calculating the Energy Values

After calculating the necessary parameters part (selecting 1 for the initial menu for the program) for the quantum well structure, one should choose 2, 3, or 4 in order to calculate the energy eigenvalues for conduction band, heavy hole band or light hole band, respectively.

3.2.2 Inputting Structure Parameters

After selecting the band to calculate the corresponding energy levels one should input:

The total number of quantum wells in the structure,
The total number of layers, which include two cladding layers, the total number of barrier and quantum well layers. In this example, there are 2 cladding + 2 barrier + 1 quantum well layers, which makes totally 5 layers.
The lowest/highest potential layer is the 1st QW layer for the conduction/valence band. In this example, layer 3 is the lowest/highest potential layer, see Fig. 3.4.1.
The center layer is layer 3 for our structure. The number of layers is always set to an odd value. For instance, if there are two quantum well layers, the total number of layers will be 7 and center layer will be 4, which is a barrier layer between two quantum well layers.

3.2.3 Selecting the Material System

This part is to select the material system of interest, which was chosen in Chapter 2 for the example. For this example material system 4 was chosen, which is InGaAlAs/InGaAlAs. That is, both the quantum well and barriers have InGaAlAs, and the cladding can be InGaAs lattice matched to InP.

3.2.4 Strain Input

For the valence band energy calculations one should provide the strain parameters. The choices are:

Strain only, if there is strain only in the quantum well.
Strain compensated, there is strain both in the quantum well and the barrier.

The detailed discussion about the strain and strain compensation is found in section 2.3. For this example, the strain compensation has been chosen, so the selection is 2. Next, the barrier strain is provided, which is 0.008776922.

3.2.5 Calculation of Energy Values

The energy values will be calculated and written in a file called energy.dat. Here it should be noted that

For the conduction band, the energy values are listed in descending order that is the first value corresponds to the first energy level and so on.
For the valence band (heavy and light hole) the order is from bottom to top. That is the bottom value corresponds to the first energy level for heavy/light hole bands.

If one runs energy calculations consecutively for energy bands without exiting the program, the energy.dat file will be appended with the new calculations. If one exits and runs the software again, this file will be overwritten.

3.2.6 Calculation of Envelope Functions and Confinement Factors

It is optional to check the Shrödinger wave functions for the corresponding energy eigenvalues. In order to obtain the envelope function for the eigenvalues

One should input 1.
Then the energy eigenvalue should be provided as an input. For instance, the energy eigenvalue for the first conduction band energy in this example is 0.480716488922E-01.
The calculated results for the envelope function and the band offset as a function of position will be written in an output file. The user should give a name for this file. In this example, cb1.dat is given as the name of the output file for the conduction band energy value 1.
Finally, the confinement factors for the layers will be calculated and displayed for the chosen energy eigenvalue envelope function.
One can continue to calculate the envelope functions for other eigenvalues by selecting 1 and following the steps from (a) in this section. Selecting 2 will end the energy calculations and bring the main menu.

3.3 Input and Output Files

3.3.1 The Input Files

In order to calculate the energy eigenvalues, there should be two input files in the directory where the program file exists (qwl.exe). These two input files are cbandeg.dat and vbandeg.dat. The detailed explanation for these files was provided in section 2.2.

3.3.2 The Output Files

For the Conduction Band, the energy eigenvalues are calculated and depicted on the screen by the program. Furthermore, an output file will be generated for the energy eigenvalues for this band, which is called energy.dat. The content of this file for the example in section 3.3.4 is as follows:

CONDUCTION BAND ENERGY===> 0.480716488922E-01 ERROR= .2389607E-14

CONDUCTION BAND ENERGY===> 0.292753578324E+00 ERROR= .3164269E-14

CONDUCTION BAND ENERGY===> 0.432969897088E+00 ERROR= .1487524E-14

CONDUCTION BAND ENERGY===> 0.483243413318E+00 ERROR= .2481610E-14

The first energy eigenvalue for the above calculation corresponds to the first line; the second energy eigenvalue corresponds to the second and so on. This is because the energy values are positive quantities in this case (above the zero reference as shown in Fig. 3.1.1); therefore, the bigger energy value corresponds to the higher energy eigenvalue.

If the Schrödinger wave function for the energy eigenvalues is asked to be calculated then an output file, whose name is to be provided by the user, will be generated. This file contains the band-offset for conduction band and the envelope function for the given energy eigenvalue. For the field envelope calculations corresponding to each eigenvalue, a separate output file is generated, which should be named by the user. For this example, they are named as cb1.dat, cb2.dat, and so on.

For the example in section 3.3.4, the file that corresponds to the first energy level eigenvalue is called cb1.dat, which contains the following values:

cb1.dat

Position Envelope Function Band-offset

-0.5101512028E+02 0.3189841262E-03 0.5859193000E+00

-0.4901512028E+02 0.4889516247E-03 0.5859193000E+00

… … …

-0.4101512028E+02 0.2699312600E-02 0.3327400000E+00

-0.3845167527E+02 0.4135554108E-02 0.3327400000E+00

… … …

-0.3076134021E+01 0.1949952187E+00 -0.4034610000E-01

0.0000000000E+00 0.1985958844E+00 -0.4034610000E-01

0.3076134021E+01 0.1949952187E+00 -0.4034610000E-01

… … …

0.3845167527E+02 0.4135554108E-02 0.3327400000E+00

0.4101512028E+02 0.2699312600E-02 0.3327400000E+00

… … …

0.4901512028E+02 0.4889516247E-03 0.5859193000E+00

0.5101512028E+02 0.3189841262E-03 0.5859193000E+00

Figure 3.3.1 is the plot for the conduction band envelope functions for energy levels 1 and 2. This is the combination of files cb1.dat and cb2.dat in this example.

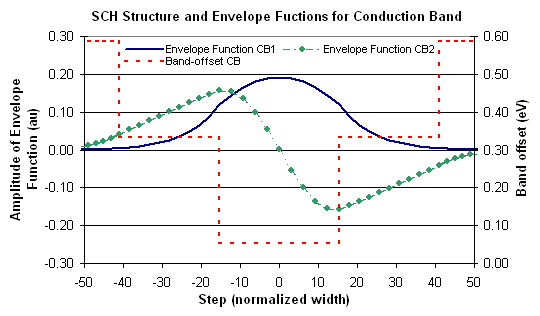
Fig. 3.3.1 Conduction band envelope functions for energy levels 1 and 2.

Similarly, for the Heavy Hole and Light Hole Bands, the energy eigenvalues are calculated and depicted on the screen by the program, and the output file, energy.dat, will be generated for the energy eigenvalues for each band.

The content of this file for the example in section 3.3.4 is as follows:

HEAVY HOLE ENERGY===> -0.223219288877E+00 ERROR= .2395481E-14

HEAVY HOLE ENERGY===> -0.185080559932E+00 ERROR= .3141766E-14

HEAVY HOLE ENERGY===> -0.175552677060E+00 ERROR= .2217630E-14

HEAVY HOLE ENERGY===> -0.118303564930E+00 ERROR= .3822063E-14

HEAVY HOLE ENERGY===> -0.232927951139E-01 ERROR= .2486083E-14

HEAVY HOLE ENERGY===> 0.400110417946E-01 ERROR= .2083172E-14

The first energy eigenvalue for the above calculation corresponds to the last line; the second energy eigenvalue corresponds to the second from bottom and so on. This is because the energy values are negative quantities for Heavy/Light Hole Band case (below the zero reference as shown in Fig. 3.1.1); therefore, the smaller negative energy value corresponds to the higher energy eigenvalue in the valence band energy levels.

If the Schrödinger wave function for the energy eigenvalues is asked to be calculated, then an output file, whose name is to be provided by the user, will be generated. This file contains the band-offset for valence band Heavy/Light Hole and the envelope function for the given energy eigenvalues. For field envelope calculations of each eigenvalue, a separate output file is generated and it should be named by the user. For this example, they are named as hh1.dat, hh2.dat and so on for the Heavy Hole Band; lh1.dat, lh2.dat and so on for the Light Hole Band. The content of these files are similar to the files for the conduction band.

Figure 3.3.2 is the plot for the heavy hole valence band envelope functions for energy levels 1, 2, and 3. This is the combination of files hh1.dat, hh2.dat, and hh3.dat in this example.

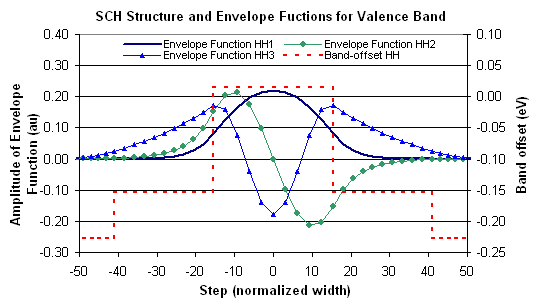
Fig. 3.3.2 Heavy hole valence band envelope functions for energy levels 1, 2, and 3.

The plots for the Light Hole Band envelope functions are similar to the plots for the Heavy Hole Band envelope functions, which are shown in Fig. 3.3.2.

3.4 Running the Software for Energy Calculations, an Example

In this Section, the energy eigenvalues will be calculated for conduction band, heavy hole band, and light hole band. The material system InGaAlAs/InGaAlAs was chosen as the example. In Chapter 2, the band offset and the material composition were calculated and the results were written to files cbandeg.dat and vbandeg.dat as an output. The detailed discussion of these files can be found in section 2.2, and for energy calculations these files are used as input files. The band offset diagrams for conduction and valence bands are shown in Fig. 3.4.1.

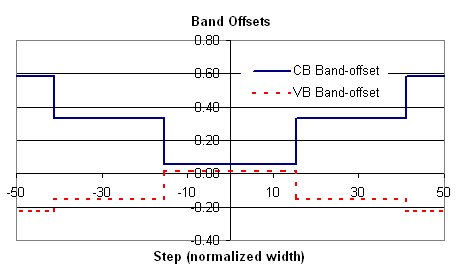
Fig. 3.4.1 Conduction Band and Valence Band offset diagram for the example.

In the following sections, 3.4.1 and 3.4.2, the software will be run continuously for the example material system for the same set of parameters chosen in section 2.3. The explanations for running the software for this example can be found in section 3.2. The explanations of input and output files for this section are in section 3.3.

3.4.1 Conduction Band Energy Calculations

The program is launched in the program folder. It provides the information about the steps in the program.

C:\Gain>qwl

************************************************************************

THE MAIN PROGRAM IS ONLY A CALLING PROGRAM, WHICH

CONTAINS THREE MAJOR PARTS (MORE THAN 20 SUBROUTINES)

FIRST SELECT MATERIAL PARAMETER,.

SECOND SELECT ENERGY LEVELS IN BOTH BANDS,

THIRD FIND THE G(J), G(WAVELENGTH) AND RATE EQUATIONS.

***********************************************************************

A. MAKING THE SELECTION TO CALCULATE THE ENERGY VALUES

This step asks for layer parameters and produces the outputs for energy eigenvalues. It also writes these values into an output file called energy.dat.

MAKE YOUR SELECTION NOW!

ENTER 1 FOR THE NECESSARY PARAMETERS

2 FOR THE ENERGY VALUES OF CONDUCTION BAND

3 FOR THE ENERGY VALUES OF HEAVY HOLE BAND

4 FOR THE ENERGY VALUES OF LIGHT HOLE BAND

5 FOR THE LASER G-J AND G(LAMBDA)

6 FOR RATE EQUATIONS (TWO SECTION MODEL INCLUDED)

7 FOR EXIT

> 2

q Note: This selects the calculation of energy values for conduction band.

B. INPUTTING THE STRUCTURE PARAMETERS

The input parameters will be provided here. The explanations for the parameters are found in section 3.2.2.

INPUT THE NUMBER OF QUANTUM WELLS NUM=?

> 1

q Note: There is a single quantum well for this example.

INPUT TOTAL LAYERS FOR STRUCTURE--N ODD

INPUT N=

> 5

q Note: Total number of layers is 5 for this structure. See Fig. 3.4.1.

INPUT THE LOWEST POTENTIAL LAYER(1st Q-WELL) IC= ?

> 3

q Note: The lowest potential layer for CB is the quantum well layer. Here the first quantum well layer is used as the input, which is layer 3.

INPUT THE SELECTED CENTER LAYER OF STRUCTURE ICR=

> 3

q Note: This is a five-layer structure. See Fig. 3.4.1.

C. SELECTING THE MATERIAL SYSTEM

The material system will be selected.

************************************************************************

INPUT I=1 FOR AlGaAs

I=2 FOR InGaAsP

I=3 FOR In1-xGaxAs/InGaAsP/InP

I=4 FOR InGaAlAs/InGaAlAs

I=5 FOR GaInP/(AlGa)0.5In0.5P/AlInP

I=6 FOR InGaAs/AlGaAs/AlGaAs

I=7 FOR InGaAs/InGaAsP/Ga0.51In0.49P(GaAs)

I=8 FOR AlyInxGa1-x-yAs/AlzGa1-zAs/GaAs

I=9 FOR InzGa1-zAs/AlxGayIn1-x-yAs/InP

I=10 FOR InGaAlAs/InGaAlAs/AlAsxSb1-x(InP)

I=11 FOR InzGa1-zAs/AlxGayIn1-x-yAs/AlAsxSb1-x

I=12 FOR In(y)Ga(1-y)As(x)N(1-x)/GaAs

I=13 FOR InGaAs/In(1-y)Ga(x)As(y)P(1-y)/GaAs

INPUT I= ?

************************************************************************

> 4

q Note: For this example material system 4 was chosen.

D. CALCULATION OF ENERGY VALUES

The energy eigenvalues are calculated and displayed on the screen. Also, they are written to an output file called energy.dat.

ENERGY EIGENVALUE ===> 0.480716488922E-01 ERROR= .2389607E-14

ENERGY EIGENVALUE ===> 0.292753578324E+00 ERROR= .3164269E-14

ENERGY EIGENVALUE ===> 0.432969897088E+00 ERROR= .1487524E-14

ENERGY EIGENVALUE ===> 0.483243413318E+00 ERROR= .2481610E-14

E. CALCULATION OF ENVELOPE FUNCTIONS AND CONFINEMENT FACTORS

This calculates the envelope functions if asked. It writes the outputs to data files whish will be named by the used.

FOR CHECKING THE Schrodinger WAVE FUNCTION INPUT I==> 1

SKIP INPUT I ==> 2

I=?

> 1

q Note: In order to calculate the envelope functions selection 1 is chosen. If 2 is selected it will skip envelope calculations.

INPUT THE EIGENVALUE

EIGEN VALUE=

> 0.480716488922E-01

q Note: This is the eigenvalue for the first energy level in CB. Any of these values can be selected to calculate the corresponding envelope functions.

INPUT THE NAME OF OUTPUT FILE

> cb1.dat

q Note: The program writes the calculation results of envelope function into this file. The user can name the file arbitrarily.

The confinement factors for each layer corresponding to the selected eigenvalue envelope function are calculated and displayed on the screen.

CONFINEMENT FACTOR OF 1 th LAYER = 0.17059025E-04

CONFINEMENT FACTOR OF 2 th LAYER = 0.46544414E-01

CONFINEMENT FACTOR OF 3 th LAYER = 0.90687705E+00

CONFINEMENT FACTOR OF 4 th LAYER = 0.46544414E-01

CONFINEMENT FACTOR OF 5 th LAYER = 0.17059025E-04

F. MORE CALCULATION FOR THE ENVELOPE FUNCTIONS AND CONFINEMENT FACTORS

In order to continue calculating the envelope functions for the energy eigenvalues of interest, Step E in this Section is repeated for each eigenvalue of interest. As an example the envelope function for second energy level is calculated below.

INPUT NEW EIGENVALUE--> 1, BACK TO MAIN PAGE--> 2

SELECT=?

> 1

q Note: To calculate the envelope function for another energy level selection 1 is chosen.

INPUT THE EIGENVALUE

EIGEN VALUE=

> 0.292753578324E+00

q Note: The energy eigenvalue of interest is provided. In this example, the value for 2nd energy level is chosen.

INPUT THE NAME OF OUTPUT FILE

> cb2.dat

q Note: This is the file that software will write calculation results. The user can choose any name.

The confinement factors for each layer corresponding to the selected eigenvalue envelope function are calculated and displayed on the screen.

CONFINEMENT FACTOR OF 1 th LAYER = 0.20929892E-02

CONFINEMENT FACTOR OF 2 th LAYER = 0.22590594E+00

CONFINEMENT FACTOR OF 3 th LAYER = 0.54400214E+00

CONFINEMENT FACTOR OF 4 th LAYER = 0.22590594E+00

CONFINEMENT FACTOR OF 5 th LAYER = 0.20929892E-02

INPUT NEW EIGENVALUE--> 1, BACK TO MAIN PAGE--> 2

SELECT=?

> 2

q Note: If Back to Main Page (selection 2) is selected the energy calculation will be terminated.

ENTER 1 FOR THE NECESSARY PARAMETERS

2 FOR THE ENERGY VALUES OF CONDUCTION BAND

3 FOR THE ENERGY VALUES OF HEAVY HOLE BAND

4 FOR THE ENERGY VALUES OF LIGHT HOLE BAND

5 FOR THE LASER G-J AND G(LAMBDA)

6 FOR RATE EQUATIONS (TWO SECTION MODEL INCLUDED)

7 FOR EXIT

> 7

q Note: This selection will terminate the program.

BACK TO FIRST SELECTION PAGE !

C:\Gain>

3.4.2 Conduction Band Heavy and Light Hole Band Energy Calculations

The Steps A, B, and C are similar to conduction band calculations in section 3.4.1.

After Step C, the strain values should be provided for both heavy hole and light hole band energy calculations.

A. STRAIN INPUT

*******************************************************

DOES THE STRUCTURE STRAIN OR STRAIN-COMPENSATED?

IF STRAIN ONLY INPUT 1, STRAIN-COMPENSATED INPUT 2

INPUT SELECT = ?

> 2

q Note: The structure in this example is strain compensated, so 2 is selected.

INPUT BARRIER STRAIN =?

> 0.008776922

q Note: This value is the strain parameter from 2.1

After providing the strain input for this step, the rest of the steps for heave hole and light hole energy calculations (Steps D, E, and F) are similar to conduction band energy calculations as in section 3.4.1.

Chapter 4 Simulations of Gain and Laser Properties

In the previous chapters, computations of material compositions, band offsets, and energy levels are discussed. After these computations, the properties of the designed semiconductor laser are simulated using the GAIN program including the simulations of the gain spectrum, threshold current density, and slope efficiency.

The basic theories involved in the simulations are discussed in ~~A.2.~~4.1, and the explanations of input and output files are provided in Sections 4.2 and 4.3 of this chapter. Finally, an example of how to run the GAIN program for gain and laser characteristics simulations is given in section 4.4.

4.1 Theories for computations of Gain and Important Laser Properties

4.1.1 Gain Calculations

The simulations of the optical gain in the active region of the lasers are complicated. The GAIN program utilizes the accurate model of the optical gain with anisotropic factor, overlap factor and Lorentz lineshape included, as shown in Equation 4.1 [3]:

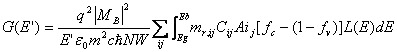(A4.2.1)

where M_B … The momentum matrix element

E … The optical energy

… Vacuum permittivity

N … Refractive index

W … Width of the well

C … The speed of light

m_r,ij … The reduced effective mass

C_ij … The overlap factor

A_ij … The anisotropic factor

f_c, f_v … The Fermi-Dirac distribution of the conduction and valence bands.

H … The step function

L(E) … The Lorentz lineshape

In the equation 4.1, the Fermi-Dirac distributions of the conduction and valence bands need to be computed. So it is necessary to calculate the quasi-fermi levels using equation 4.2 for conduction band and equation 4.3 for valence band [4].

, (4.2)

(4.3)

where N is the carrier concentration of the electrons in the conduction band,

P is the carrier concentration of the holes in the valence band,

are quasi-fermi levels,

m^*_nand m^*_lh,hh are the in-plane effective masses of the electrons and holes,

L_z is the quantum well width,

k is the Boltzmann constant, and

is the reduced plank constant.

In the above equations 4.2 and 4.3, the quasi-fermi levels can be solved with a given carrier concentration, and known energy levels which have been calculated in the previous steps of GAIN program.

In summary, from the above equations, the Optical/Mode Gain as a function of wavelength and Optical/Mode Gain as a function of photon energy are computed. The example of how to run the GAIN program to get the results is shown section 4.3 of this Chapter.

4.1.2 Threshold Current Density (Jth) and Slope Efficiency Calculations

4.1.2.1 Threshold Current Density (Jth) Calculations:

The GAIN program provides two threshold current densities (Jth) of the designed laser that correspond to two different methods. The first method is to match the threshold condition [5], and the second method is to use McIlroy theory [5]. This subsection gives the brief introduction of the two methods.

1. Threshold condition method.

In order for the laser to lase, the mode gain which is the product of the optical gain and confinement factor has to overcome the total loss which is the sum of the material loss and mirror loss, as shown in Equation 4.4. The GAIN program finds the current density at which the mode gain overcomes the loss to be the threshold current density of the laser structure [5].

In this method, the GAIN program first simulates the threshold current density for a single quantum well structure, and then use the product of the number of quantum wells and the threshold current density of the single quantum well to approximate the threshold current density of the multiple quantum well, as shown in equation 4.5.

(4.4)

J_th-MQW = n * J_th-SQW (4.5)

where n: number of quantum wells,

a_i: intrinsic loss,

L: cavity length,

R₁, R₂: reflectivities of the facets.

2. McIlroy method.

For the McIlroy method, the threshold current density is approximated by the empirical equation 4.6 [5]:

(4.6)

where Jo is obtained in Figure 4.1.1, and the optimum number of quantum wells (N_opt) is calculated by equation 4.7 [5]:

(4.7)

where Go is acquired in Figure 4.1.1,

G_sqw is the confinement factor of a single quantum well,

a_i: intrinsic loss,

L: cavity length,

R₁, R₂: reflectivities of the facets.

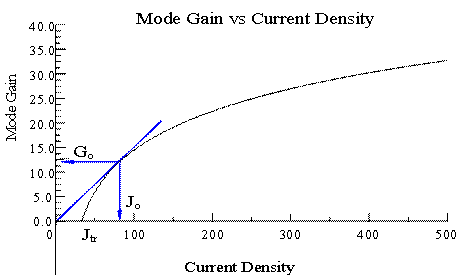
Fig. 4.1.1. Mode gain as a function of current density for a single QW structure.

4.1.2.2 L-I Curve and Slope Efficiency Calculations

The optical output power of the laser as a function of injected current and the slope efficiency is simulated in GAIN program [6] using the equation 4.8.

(4.8)

where P: the output power of the laser

a_i: intrinsic loss

a_m: mirror loss

h_i: internal quantum efficiency

W: width of the quantum well

L: length of the quantum well

n: photon frequency

J_th: threshold current density

q: elementary charge

h: plank constant

R₁, R₂: reflectivities of the facets.

The slope efficiency can be calculated from the L-I curve DP/DI, as shown in Figure 4.1.2.

Text Box: Slope Efficiency = DP/DI mW/mA

Figure 4.1.2 L-I curve of the laser

4.2 Input File

The input file is needed at the beginning of the step 5 of the gain program. It includes the basic input data for the laser structure such as the compositions, width of well, effective index, lasing wavelength, the energy levels etc. In the following, the input file is broken into 6 parts to give detail explanation.

Note: Here we use the material system No. 4 ( AlGaInAs/InP ) as an example.

Part 1:

cccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccc

c 1. Input the compositions, width of well, effective index c

c and lasing wavelength. c

c Ex: xx,xz,qy,xy,lx,n,lam c

c for different materials the following are the forms of inputs. c

c c

c w -- > well, b -- > barrier cxz and cxy for cladding. c

c c

c a. AlxGa1-xAs : xx (Al w) xz (Al b) qy (0) xy (0) c

c b. In1-xGaxAsyP1-y : xx (Ga w) xz (Ga b) qy (As w) xy (As b) c

c c. In1-xGaxAs/InGaAsP : xx (Ga w) xz (Ga b) qy (0) xy (As b) c

c d. AlxGayIn1-x-yAs/InP : xx (Ga w) xz (Ga b) qy (Al w) xy (Al b)c

c e. c

c f. InxGa1-xAs/AlGaAs : xx (In w) xz (0) qy (0) xy (Al b) c

c g. c

c h. AlyInxGa1-x-yAs/AlGaAs : xx (Al w) xz (al b) qy (In w) xz (0)c

c i. In1-xGaxAs/AlGaInAs : xx (In w) xz (0) qy (Al b) xy (Ga b) c

c j. In(y)Ga(1-y)As(x)N(1-x) :xx(As w),xz(As, b),qy(In w),xy(In b)c

c k. InGaAs/InGaAsP/GaAs: xx (In w), (0), xz(Ga w) xy (As b)

cccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccc

0.21964924 0.34879557 0.0801355 0.2505339 6.0 3.218741 1.5

NOTE for Part 1 of the Input File:

(a):Here we use the material system AlGaInAs/InP as an example.

(b):The first 4 numbers come from the file cbandeg.dat or vbandeg.dat, which are the output files of step 1 ( explained in chapter 2 ). The order is: quantum well x composition, barrier x composition, quantum well y composition, barrier y composition. Ps: Please refer to the Appendix for the definition of x and y which are different for different material systems.

(c): The width of well should be chosen in a reasonable ra

nge, the effective index can be got by using the WAVEGUIDE or MODEIG software or refer to some book to calculate.

(d): The units of the width of quantum well and the lasing wavelength are nm and um.

Part 2:

cccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccc

c 2. Input the energy gap,temperature, barrier band edges(both bands)

c Ex: eg,temp,ec,ev c

cccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccc

0.683804 298 0.3327401 0.1241536

NOTE for Part 2 of the Input File:

(a): Energy gap here refer to the QW Eg, which is equal to 1.24/quantum well wavelength (um), this is calculated in the step 1 of the gain program.

(b): Enter the temperature, please note that the material loss, optical Auger coefficient, and other parameters need to be adjusted for different temperature.

(c): Find the barrier band edges for both conduction and valence bands from the output files of the step 1: cbandeg.dat and vbandeg.dat. The barrier band edge of the valence band should change to the opposite sign value of the real number.

Part 3:

cccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccc

c 3. Input the ist level sub-band energy levels. c

c Ex: ec1,eh1,el1 c

cccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccc

0.132273291719 0.584032029186E-02 0.978425521147E-01 1 1 1

NOTE for Part 3 of the Input File:

(a): The order of the input data is: the first energy levels of conduction, heavy hole, light hole and the second energy levels of conduction, heavy hole, light hole. These data come from the step 2, 3 and 4 of the gain program, which are calculated from the step 2, 3, and 4, and can be found in the output file: energy.dat.

(b): The values from the heavy hole and light hole should change to the opposite sign value of the real number.

(c): If the second energy levels of conduction are above the barrier band edge, use 1 to replace the value of ec2; if the second energy levels of valence band are under the barrier band edge, use 1 to replace the value of eh2 or el2.

Part 4:

cccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccc

c 4. Input the material loss, reflectivities, number of quantum c

c wells and beta(for spontaneous emission). c

c Ex: alpha,r1,r2,mm,beta. c

cccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccc

12.0d0 0.30 0.30 1 5.D-5

NOTE for Part 4 of the Input File:

These values are good for starting.

(1): The loss and reflectivity (r1, r2) are key factors to determine the threshold condition.

(2): If the number of quantum wells (mm) is more than one, then the output files

*.gjr and *.gja will calculate the G-J file for multiple wells which is not necessary.

(3): The beta is only used in dynamic calculation and this number here is an advised parameter for ridge and BH laser simulations.

Part 5:

cccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccc

c 5. Input the cavity length, ridge width, internal efficiency c

c Auger, strain(except AlGaAs,put 0) and confinement factor. c

c Ex: cl,cw,etha,ca,es,confine c

cccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccc

750.D-4 3D-4 0.96 1.00d-29 0.000 0.009834488

NOTE for Part 5 of the Input File:

(a): The cavity (cl) and width (cw) of ridge are structure features, the units of cavity length and ridge width are cm.

(b): The internal efficiency (etha) and Auger (ca) can refer to papers for the latest values.

(c): The strain (es) is just ignored for all material systems except for GaAs/AlGaAs)

(d): Give the initial guess of the confinement factor of the quantum well.

Part 6:

cccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccc

c 6. Input the cladding composition and band edges. c

c Ex: cxz,cxy,ecc,evv c

cccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccc

0.48 0.0 0.5859193 0.2278575

NOTE for Part 6 of the Input File:

Find the cladding composition (cxz and cxy) and the band edges (ecc and evv) from the cbandeg.dat or vbandeg.dat, the band edges from the vbandeg.dat should change to the opposite sign value of the real number.

4.3 Output files

There are total 17 output files containing important laser information from the step 5 of the gain program. Table 4.1 shows details, and the plots of the output files are also provided in 4.3.2.

4.3.1 The table for the Output Files.

Table 4.3.1 : The table for the output files.

File name	Content	X axis	Y axis
Cfermil	Quasi Fermi-level for conduction band	Number of N-carrier (/cm³)	C band Quasi Fermi Level (eV)
Vfermil	Quasi Fermi-level for valence band	Number of P-carrier (/cm³)	V band Quasi Fermi-Level (eV)
****.ant	Anti-guiding factor as function of current density	Current Density (A/cm²)	Anti-guiding Factor
****.cp	Gain compression	carrier density (*E18)	Gain compression (cm³)
****.dg	Differential gain	Carrier density (*E18)	Differential Gain (cm²)
****.gc	Peak material gain as function of carrier density	Carrier density (*E18)	Peak Material Gain (1/cm)
****.gja	Peak material gain as function of threshold current density	Current Density (A/cm²)	Peak Material Gain (1/cm)
****.gjr	Peak mode gain as function of current density	Current Density (A/cm²)	Peak Mode Gain (1/cm)
****.lek	Leakage current as function of carrier concentration	Leakage Current (A/cm²)	Carrier Concentration (1/cm³)
****.ric	Carrier induced refractive index change	Number of Carrier	Refractive Index Change
****.pi	P-I relation: use single well times # of wells.	Power (mW)	Current (mA)
****.pi2	P-I relation: use McIlory method for single well,Then with Nopt	Power (mW)	Current (mA)
****.rq	Relaxation oscillation frequency as function of J (above J^th)	Current Density (A/cm²)	Relaxation Oscillation Frequency (Hz)
COGL.txt	Convolution optical gain (lambda)	Lasing Wavelength (μm)	Material Gain (1/cm)
CMGL.txt	Convolution mode gain (lambda)	Lasing Wavelength (μm)	Mode Gain (1/cm)
COGE.txt	Convolution optical gain (E)	Photon Energy (eV)	Material Gain (1/cm)
CMGE.txt	Convolution mode gain (E)	Photon Energy (eV)	Mode Gain (1/cm)

NOTE: The four names and extensions of txt files: COGL.txt, CMGL.txt, COGE.txt and CMGE.txtare entered by the users.

4.3.2 The Drawings for the Output Files.

There are 17 figures according to the 17 output data files that generated from the step 5 of the Gain program as following:

Fig 4.3.2.1: cfermil Fig 4.3.2.2: vfermil

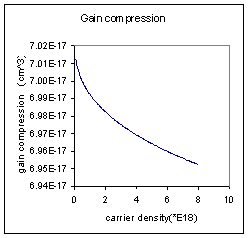
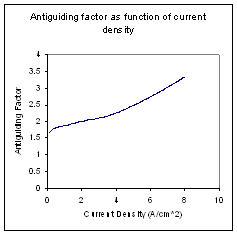
Fig 4.3.2.3: ****.ant Fig 4.3.2.4: ****.cp

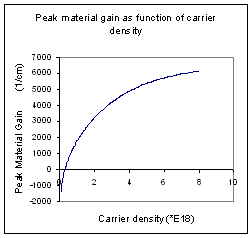
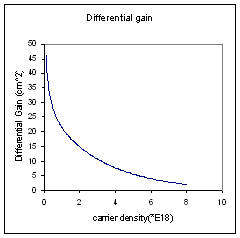
Fig 4.3.2.5: ****.dg Fig 4.3.2.6: ****.gc

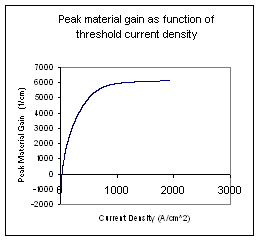
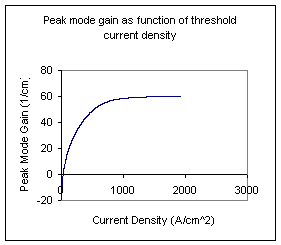
Fig 4.3.2.7: ****.gja Fig 4.3.2.8: ****.gjr

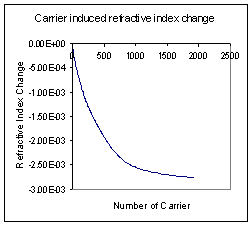
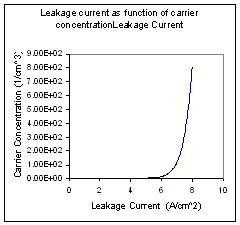
Fig 4.3.2.9: ****.lek Fig 4.3.2.10: ****.ric

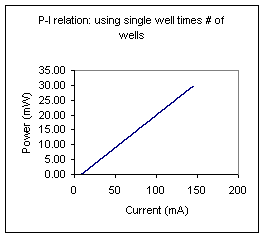
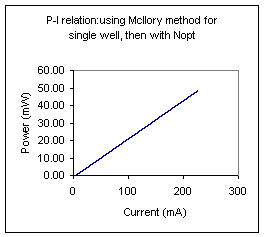
Fig 4.3.2.11: ****.pi Fig 4.3.2.12: ****.pi2

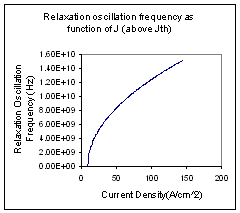
Fig 4.3.2.13: ****.rq

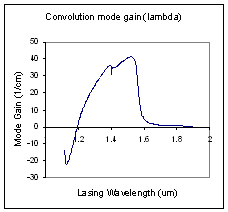
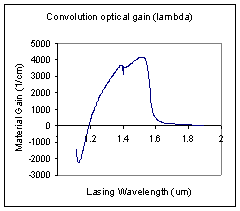
Fig 4.3.2.14: COGL.txt Fig 4.3.2.15: CMGL.txt

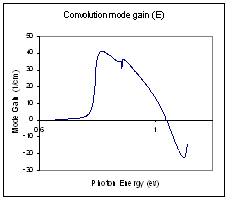
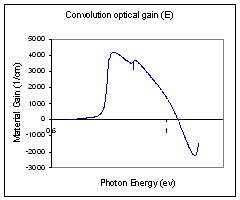
Fig 4.3.2.16: COGE.txt Fig 4.3.2.17: CMGE.txt

4.4 Running the Software for Gain and Laser Characteristics

In this section, an example will be shown to explicate the steps of running the 5th part of the Gain program “FOR THE LASER G-J AND G (LAMBDA)”. To run this part, the previous 4 parts must be followed in order to get the required parameters and input files. Detailed steps are shown below:

THE INPUT FILE NAME=

> in1.tex-----------------------or any other name of a txt file.

Ø Note: The file “in1.tex” is built based on the output from previous 4 parts. The detailed description about the contents of the input file and how to build them are already given in section 4.2 “input file”.

SELECT MATERIAL=?

1--AlGaAs

2--InGaAsP

3--In1-zGazAs/InGaAsP/InP

4-- InGaAlAs

5--GaInP/AlzGawIn1-z-wP/Al0.5In0.5P

6-- InxGa1-xAs/AlxGa1-xAs/AlGaAs

7--In1-xGaxAs/InGaAsP/GaxIn1-xP(X=0.51) MATCHED TO GaAs

8--AlyInxGa1-x-yAs/AlzGa1-zAs/GaAs

9--InzGa1-zAs/AlxGayIn1-x-yAs/InP

10-- InGaAlAs/InGaAlAs/AlAsSb

11--InzGa1-zAs/AlxGayIn1-x-yAs/AlAsSb

12--In(y)Ga(1-y)As(x)N(1-x)/GaAs

13--InGaAs/In(1-x)Ga(x)As(y)P(1-y)/GaAs

INPUT SELECTION

> 4-----------------------or any other material type

Ø Note: In order to keep the consistency, the material selected here is the same as the material system used in the examples given in previous chapters.

INPUT MODE = ? FOR TE--> MODE =1, FOR TM--> MODE =2

INPUT TE OR TM ?

> 1

Ø Note: TE and TM are two kinds of electromagnetic field modes. TE refers to transverse-electric, and TM means transverse-magnetic.

IF EL1 BELOW EH1 THEN SELECT 1, OTHERWISE SELECT 2

SELECTION=?

> 1

Ø Note: EL1 refers to the energy of 1^st light hole valence band. EH1 refers to the energy of 1^st heavy hole valence band. From the file “energy.dat” generated from previous parts 3-4, we can find EL1 = -0.897913179665E-01, and EH1 = -0.153962179517E-02. Since EL1 < EH1, we select 1.

************************************************************************ CALCULATE THE EFFECTIVE MASS ************************************************************************

FOR QUASI-FERMI LEVEL SELECT=1,

FOR READ EXISTING QUASI-FERMI LEVEL SELECT=2

SELECT=?

> 1

Ø Note: In most cases, “1” is selected. If a file of quasi-fermi level is already existed and there is no any change to those parameters of the laser structure, “2” can be selected to save the calculation time.

After that, quasi-fermi level is calculated and two output files “cfermil.dat” and “vfermil.dat” are generated. In addition, another eight files named “in1.tex.ant”, “in1.tex.cp”, “in1.tex.dg”, “in1.tex.gc”, “in1.tex.gja”, “in1.tex.gjr”, “in1.tex.lek” and “in1.tex.ric” are generated too. Then, values for G(J), G(N), Jtr, Ntr and the optimum number of quantum well are shown up. The meaning and usage of those files are explained in section 4.1 “Theories for computation of Gain and Laser properties” and section 4.3 “output files”.

************************************************************************

J(LEAKAGE)=0.811020D-02 A/cm^2 N=0.239674D+19 1/cm^3

J(LEAKAGE)=0.845424D-02 A/cm^2 N=0.241654D+19 1/cm^3

……

J(LEAKAGE)=0.784174D+03 A/cm^2 N=0.798020D+19 1/cm^3

J(LEAKAGE)=0.812685D+03 A/cm^2 N=0.800000D+19 1/cm^3

************************************************************************

G(J) PARAMETERS FROM SINGLE WELL

Go=0.158181D+02 1/cm Jo=0.954942D+02 A/cm^2

G(N) PARAMETERS FROM SINGLE WELL

NGo=0.160843D+04 1/cm XNo=0.911779D+18 1/cm^3

Jtr=0.351304D+02 A/cm^2 NTR=0.335425D+18 1/cm^3

THE OPTIMUM NUMBER OF QUANTUM WELL FOLLOWS THE ARTICLE

BY McIlory et al. IEEE JQE-21 1985.

THE OPTIMUM NUMBER OF QUANTUM WELL Nopt = 2

INPUT Nopt(CAN BE DIFFERENT FROM ABOVE CALCULATION)=?

> 1

Ø Note: This is the optimum number of quantum well.

NUMBER OF QUANTUM WELL (MAY OR MAY NOT BE Nopt)=?

> 1

Ø Note: This is the number of quantum well designed by the users.

Ø Here, files named “in1.tex.pi”, “in1.tex.pi2”, and “in1.tex.rq” are generated in the same directory. After that, threshold current density “Jth”, threshold current “Ith” and the slope efficiency “B” are calculated out. Detailed explanation for threshold current density, threshold current and the slope efficiency can be found in section 4.1.2.

The output are shown below.

************************************************************************

1ST CHECK USE SINGLE WELL TIMES # OF WELLS

************************************************************************

2ND CHECK FOLLOWS FORMULA BY McIlory IN IEEE

JOURNAL OF QUANTUM ELECTRONIC QE-21 1985.

**************************************************

Gth= 28.0530 1/cm Nth=0.170376D+19 1/cm^3 IY= 82

1ST CHECK Jth= 190.71442056 A/cm^2

2ND CHECK Jth= 99.47316 A/cm^2

1ST CHECK Ith=0.429107D+01 mA NUMBER OF WELLS= 1

2ND CHECK Ith=0.223815D+01 mA

************************************************************************CALCULATE THE P-I RELATION

NDATA= 319

************************************************************************

CALCULATE THE SLOPE: mW/mA Y=A+BX

CONSTANT A= -0.9372099 SLOPE B= 0.2184091

Ø Note: 1^st method checks the threshold condition and the G-J curves and then decides the Jth and others. The 2^nd check is strictly following the Maclloy theory. Detailed explanation for these two methods can be found in section 4.1.2.

***********************************************************************

INPUT POWER PO FOR THE LINEWIDTH, PO=0 FOR STOP

INPUT PO = mW

> 0

Ø Note: Because of the updating of new method, Line width calculation is not recommended here. New version of software is under construction.

INPUT 1 FOR THE DYNAMIC CALCULATION. 2 FOR SKIP

INPUT =

> 2

Ø Note: New version of dynamic calculation is under construction.

K-FACTOR= 0.33294 nS MAXIUM FREQ.= 26.6891 GHz

************************************************************************

INPUT 1 FOR CALCULATE THE GAIN(E) RELATION.

INPUT 2 FOR CALCULATE THE LINEWIDTH ENHENCEMENT

FACTOR AND PHOTON ENERGY RELATION

INPUT 3 FOR EXIT THE PROGRAM

THE INPUT # IS

> 1

Ø Note: The calculation of line width enhancement factor and photon energy relation is not recommended here. New version of software is under construction.

INPUT FERMILEVELS IN C-BAND, V-BAND, AND CARRIER DENSITY

> 0.238566456069E+00, 0.666558305734E-02, 2E+18

Ø Note: These values come from the two output files “cfermil.dat” and “vfermil.dat” generated in the previous steps. Based on the different carrier density, the corresponding C-band and V-band fermi-level values can be found in those two files.

CALCULATE THE CONVOLUTION GAIN (E) COEFFICIENT

************************************************************************

INPUT THE NAME FOR THE CONVOLUTION OPTICAL GAIN(LAMBDA)

> opticalgain

Ø Note: Input any name you like for the file of optical gain.

************************************************************************

INPUT THE NAME FOR THE CONVOLUTION MODE GAIN(LAMBDA)

> modegain

Ø Note: Input any name you like for the file of mode gain.

INPUT THE NAME FOR THE CONVOLUTION OPTICAL GAIN(E)

> opticalgaine

Ø Note: Input any name you like for the file of optical gain (E).

************************************************************************

INPUT THE NAME FOR THE CONVOLUTION MODE GAIN(E)

> modegaine

Ø Note: Input any name you like for the file of mode gain (E).

************************************************************************

INPUT 1 FOR REPEAT THE G(E) CALCULATION

INPUT 2 FOR REPEAT THE ALPHA(E) CALCULATION

INPUT 3 FOR EXIT

> 3

Ø Notes: New version of the alpha (E) calculation is under construction.

Appendix A Material Parameters

This section provides the information of every material system used in GAIN software on:

1. Materials used for QW, barrier, cladding and substrate.

2. The equations used for calculating the material compositions of quantum well (QW), barrier and cladding layers. In these equations, the energy gap corresponds to that of bulk materials. The designer should adjust the energy gap and layer thicknesses to get the required lasing wavelengths. Usually this process will be repeated several times for a satisfying design.

3. Numerical methods used in calculating the material compositions. The detailed information on the numerical methods is beyond this manual. Please reference to book [10], [11] for more information on the numerical methods.

4. Practical lasing wavelengths for each material system. Usually a specific material system can cover a specific range of lasing wavelength. However, in this manual we give the practically widely used lasing wavelengths for some material systems. The user can design the semiconductor laser device with reference to the practical lasing wavelengths for each material system.

If not explicitly tell, the units of wavelength, energy gap, layers width, and lattice constant for all the material systems are mm, eV, Å, Å, respectively.

Table A.1 gives the composition of different parts of the quantum well laser structure

Table A.1 The composition of materials in quantum well, barrier, cladding and substrate.

Materia System	Quantum Well	Barrier	Cladding	Substrate
1	AlGaAs	AlGaAs	AlGaAs	GaAs
2	InGaAsP	InGaAsP	InGaAsP	InP
3	InGaAs	InGaAsP	InP	InP
4	InGaAlAs	InGaAlAs	InGaAlAs	InP
5	GaInP	(AlGa)0.5In0.5P	AlInP	GaAs
6	InGaAs	AlGaAs	AlGaAs	GaAs
7	Be substituted by13
8	AlInGaAs	AlGaAs	GaAs	GaAs
9	InGaAs	AlGaInAs	AlGaInAs	InP
10	InGaAlAs	InGaAsAs	AlAsSb	InP
11	InGaAs	AlGaInAs	AlAsSb	InP
12	InGaAsN	GaAs(dilute N)	GaAs (dilute N)	GaAs
13	InGaAsP	InGaAsP	GaAs	GaAs

1 AlGaAs/AlGaAs (Substrate: GaAs)

Form of composition: AlxGa1-xAs/AlyGa1-yAs

Parameters to be input: Bulk material wavelengths of QW, barrier and cladding, widths of conduction band, valence band and QW.

Lasing wavelength: <870nm

Screen output: Band gap of QW

Equation for calculating x by wavelength:

Method Used: Direct method

2 InGaAsP/InGaAsP (Substrate: InP)

Form of composition: In1-xGaxAsyP1-y, in output read Ga first then As

Parameters to be input: Bulk material wavelengths of QW, barrier and cladding, widths of conduction band, valence band and QW, strains of quantum well and barrier.

Lasing wavelength: 1.2mm -1.7um

Screen output: Strain, band gap of QW

Equation for calculating x and y by wavelength:

(Å)

When lattice-matched to InP

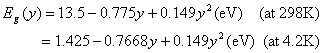
Method Used: Damped Newton method for the nonlinear systems of equations.

3 InGaAs/InGaAsP/InP (Substrate: InP)

Form of composition: In1-xGaxAs/ In1-xGaxAsyP1-y

Parameters to be input: Wavelength the correspond to the band gap, widths

Lasing wavelength: 1.2mm -1.7um

Screen output: Strain, band gap of QW

Equation for calculating x and y by wavelength:

For InGaAs:

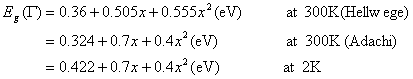
We are using Hellwege Formula here.

For InGaAsP:

(Å)

When lattice-matched to InP

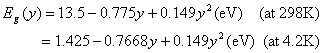
Method Used: Damped Newton method for the nonlinear systems of equations.

4 InGaAlAs/InGaAlAs (Substrate: InP)

Form of composition: AlyGaxIn(1-x-y)As, in output read Ga first then Al

Parameters to be input: Wavelengths, strain (Can be compressive or tensile). If one of the components in active region is zero, the initial guess for wavelength and strain.

Lasing wavelength:1.3um, 1.55um, 1.6um

Screen output: Strain, band gap of QW

Equation for calculating x and y:

Where

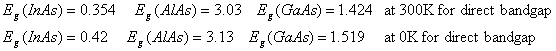
In this material system, we have two selections; 1^st Eg relation based on the text book by Dr. Chuang and the 2^nd one based on industrial experimental formula.

Method Used: Damped Newton method for the nonlinear systems of equations.

5 GaInP/(AlGa)0.5In0.5P/AlInP (Substrate: GaAs)

Form of composition: GaxIn1-xP, AlxIn1-xP

Parameters: Wavelengths and widths, short wavelength

Lasing wavelength: red (about 630nm)

Screen output: Band gap of QW, strain in GaInP

Equation to calculate x and strain:

For GaInP:

Not available yet

For AlxIn1-xP

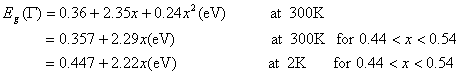
Method Used: Direct method.

6 InGaAs/AlGaAs/AlGaAs (Substrate: GaAs)

Form of composition: In1-xGaxAs/AlyGa1-yAs

Parameters to be input: Wavelengths

Lasing wavelength: 980nm

Screen output: Band gap of QW. Strain for InGaAs/AlGaAs

Equation for calculating x or y:

For InGaAs:

For AlGaAs(x<0.4 ):

Method Used: Direct method.

7 InGaAs/InGaAsP/Ga0.51In0.49P (Substrate: GaAs)

This material system is not used any more and is substituted by material system 13.

8 AlyInxGa1-x-yAs/AlzGa1-zAs/GaAs (Substrate: GaAs)

Form of composition: AlyInxGa1-x-yAs/AlzGa1-zAs/GaAs

Parameters to be input: Wavelengths, Y and X values

Lasing wavelength: 808nm-980nm

Screen output: Band gap of QW. BANDGAP again, WELL LATTICE, BARRIER LATTICE, STRAIN

Equations for calculating x, y and z:

For AlInGaAs

Where

For AlGaAs

Please substitute x by z for AlGaAs. In the future z has the same meaning as x in material composition formulas.

Method Used: Damped Newton method for the nonlinear systems of equations.

9 InzGa1-zAs/AlxGayIn1-x-yAs/AlxGayIn1-x-yAs(Substrate: InP)

Form of composition: InzGa1-zAs/AlxGayIn1-x-yAs/InP

Parameters: Wavelengths

Lasing wavelength: 1.3um, 1.55um, 1.6um

Screen output: Band gap of QW

CALCULATE THE In(z)Ga(1-z)As QUANTUM WELL--Z

BARRIER Al(x)Ga(y)In(1-x-y)As AND

CLADDING Al(xc)Ga(yc)In(1-xc-yc)As

X,Y--FOR BARRIER,XC,YC--FOR CLADDING and Z

CHECK STRAIN= 1.289076522918892E-002

Equation for calculating x, y and z:

For InGaAs

For AlInGaAs

Where

Method Used: Direct method

10 InGaAlAs/InGaAlAs/AlAsxSb1-x (Substrate: InP)

Form of composition: AlyGaxIn1-x-yAs/ AluGavIn1-u-vAs/AlAszSb1-z

Parameters to be input: Compress or tensile, J=, strain

Lasing wavelength: Long wavelength (>1.3um)

Screen output: Band gap of QW, THE MATCHED BARRIER AND CLADDING COMPOSITION

X,Z--FOR BARRIER,XC,ZC--FOR CLADDING

Equations for calculating x, y/(u, v) and z by wavelength:

For AlInGaAs

Where

For AlAsSb

Not available yet.

Here z has the same meaning as x in material composition.

Method Used: Not available yet.

11 Ga1-zAs/AlxGayIn1-x-yAs/AlAsxSb1-x (Substrate: InP)

Form of composition: In(z)Ga(1-z)As, Al(x)Ga(y)In(1-x-y)As, AlAs(xc)Sb(1-xc)

Parameters to be input: wavelengths

Lasing wavelength: 1.3um

Screen output: The band gap of QW

X, Y--FOR BARRIER, XC, YC--FOR CLADDING, STRAIN

Equations for calculating x, y z and xc:

For InGaAs:

We are using Hellwege Formula here.

For AlInGaAs

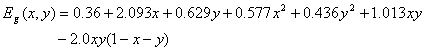
Where

For AlAsSb:

Not available yet.

Method Used: Not available yet.

12 In(y)Ga(1-y)As(x)N(1-x)/GaAs (dilute N) (Substrate GaAs)

Form of composition: InyGa1-yAsxN1-x

Parameters to be input: wavelengths, strain

Lasing wavelength: 1.3um

Screen output: Band gap of QW, strain vector, strain, AZ2

Equation for calculating x:

For InGaAsN

Method Used: Damped Newton method for the nonlinear systems of equations.

13 In(1-x)Ga(x)As(y)P(1-y)/GaAs (Substrate GaAs)

Form of composition:

Quantum well In(1-x)Ga(x)As(y)P(1-y), Barrier In(1-y)Ga(y)As(x)P(1-x)

Parameters to be input: Wavelengths

Lasing wavelength: 980nm

Screen output: STRAIN FOR InGaAs/InGaAsP/GaAs,

Equation for calculating x and y:

For InGaAsP

(Å)

When lattice-matched to GaAs

Method Used: Bauhuber method.

Appendix B Complex Structure Examples

Two examples demonstrate how to generate CBANDEG.DAT and VBANDEG.DAT files using the “GAIN” software. One example is a single-quantum-well laser with GRIN structure, and the other is a multiple-quantum-well laser with GRIN structure.

B.1 A 1.55μm InGaAlAs/InP compressive strained Single-Quantum-Well laser with GRIN structure

This example shows how to generate CBANDEG.DAT and VBANDEG.DAT files for a single-quantum-well laser with GRIN structure. Five steps, consisting of Select functions, Select materials, Input the structure parameters, Input strain, and Check output files, are involved in this procedure. After completing these five steps, we can find CBANDEG.DAT and VBANDEG.DAT in the current directory. Table B.1.1 summarizes input parameters.

TABLE B.1.1 Input parameters

Layers	l ( (μm))	Strain	Length (Å)
QW (InGaAlAs)	1.56	-0.0117	100
Barrier (InGaAlAs)	1.3	0	100
Cladding (InGaAlAs)	1.1		1000

Step 1: Select function

ENTER

1 FOR THE NECESSARY PARAMETERS

2 FOR THE ENERGY VALUES OF CONDUCTION BAND

3 FOR THE ENERGY VALUES OF HEAVY HOLE BAND

4 FOR THE ENERGY VALUES OF LIGHT HOLE BAND

5 FOR THE LASER G-J AND G(LAMBDA)

6 FOR RATE EQUATIONS(TWO SECTION MODEL INCLUDED)

7 FOR EXIT!

Note: To input the necessary parameters shown in table I

Step 2: Select material

ENTER

1 FOR AlGaAs/AlGaAs

2 FOR InGaAsP/InGaAs

3 FOR InGaAs/InGaAsP/InP

4 FOR InGaAlAs/InGaAlAs

5 FOR GaInP/(AlGa)0.5In0.5P/AlInP

6 FOR InGaAs/AlGaAs/AlGaAs

7 FOR InGaAs/InGaAsP/Ga0.51In0.49P(MATCHED GaAs)

8 FOR AlyInxGa1-x-yAs/AlzGa1-zAs/GaAs

9 FOR InzGa1-zAs/AlxGayIn1-x-yAs/InP

10 FOR InGaAlAs/InGaAlAs/AlAsxSb1-x(matched InP)

11 FOR InzGa1-zAs/AlxGayIn1-x-yAs/AlAsxSb1-x

12 FOR EXIT, BACK TO MAIN PAGE!

Note: Select the material system. This example uses InGaAlAs/InGaAlAs , we select number 4

Step 3: Input the structure parameters

INPUT THE LAYER # FOR GRIN STRUCTURE(STEP)

STEP N=

Note: Input the number of the Separate Confinement Heterostructure (SCH) layer. This example uses a 10-step SCH layer in each side of the quantum well, and the input value is 11 (10+1). If the designed laser has no GRIN structure, the input value is 2.

INPUT THE WELL WAVELENGTH (μm)

1.56

Note: Input the wavelength 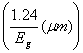, where is the energy bandgap of the active material. This value must be larger than the desired lasing wavelength.

INPUT THE BARRIER WAVELENGTH (μm)

1.3

Note: Input the barrier wavelength. This value must be smaller than the desired lasing wavelength.

INPUT THE CLADDING WAVELENGTH (μm)

1.1

Note: Input the cladding wavelength. This value must be smaller than the Barrier wavelength.

INPUT CLADDING, BARRIER, QUANTUM WELL WIDTH (Å)

1000 100 100

Note: Input the width of the cladding layer, the barrier and the quantum well. Each item is separated by a space. Generally, the width of the quantum well should be smaller than 150 Å.

FOR AlyGaxIn(1-x)As, in output read Ga first then Al

IF ONE OF THE COMPONENTS IN ACTIVE REGION IS ZERO

YOU HAVE TO TRY ANOTHER INITIAL GUESS FOR

BOTH WAVEKLENGTH AND STRAIN

Step 4: Input strain

INPUT STRAIN

-0.0117

Note: Input strain in the quantum well. If the lattice constant of the quantum well is larger than that of the substrate (compressive strain), the input value is negative. On the contrary, it is called tensile strain, and the input value is positive.

FOR Eg relation from Dr. Chuang’s book input 1,

for Industrial experimental formula input 2

INPUT =à?

Note: Select the method to calculate the bandgap energy. Both methods can be used in the calculation.

FOR BARRIER IS LATTICE MATCHED SELECT ==>1

FOR BARRIER IS STRAIN COMPENSATED SELECT ==>2

SELECTION IS==>

WRITE CONDUCTION BAND PARAMETERS INTO CBANDEG.DAT

WRITE VALENCE BAND PARAMETERS INTO VBANDEG.DAT

INPUT 1 FOR NEW CALCULATION

2 FOR EXIT

INPUT =?

Step 5: Check output f files, CBANDEG.DAT and VBANDEG.DAT

Note: After completing the last four steps, we obtain the CBANDEG.DAT and VBANDEG.DAT in the current directory. Some information, such as strain, lattice constant, width of each region, the calculated material composition, and band offset, are included in both files. Before a new design, it is prefer to delete the old files named CBANDEG.DAT and VBANDEG.DAT.

CBANDEG.DAT(conduction band structure)

strain lattice constant(quantum well)

-.117000E-01 0.596875E-09

width of each region material composition (x y) band offset (e.V)

0.10000000E+04 0.22628379E+00 0.2437162 0.2393287

0.10000000E+02 0.23436627E+00 0.2359803 0.2268420

0.10000000E+02 0.24244875E+00 0.2282444 0.2143553

0.10000000E+02 0.25053123E+00 0.2205085 0.2018685

0.10000000E+02 0.25861371E+00 0.2127726 0.1893818

0.10000000E+02 0.26669619E+00 0.2050367 0.1768951

0.10000000E+02 0.27477867E+00 0.1973008 0.1644084

0.10000000E+02 0.28286115E+00 0.1895649 0.1519217

0.10000000E+02 0.29094363E+00 0.1818290 0.1394350

0.10000000E+02 0.29902611E+00 0.1740931 0.1269483

0.10000000E+02 0.30710859E+00 0.1663572 0.1144615

0.10000000E+03 0.14346182E+00 0.1576771 0.0526335

0.10000000E+02 0.30710859E+00 0.1663572 0.1144615

0.10000000E+02 0.29902611E+00 0.1740931 0.1269483

0.10000000E+02 0.29094363E+00 0.1818290 0.1394350

0.10000000E+02 0.28286115E+00 0.1895649 0.1519217

0.10000000E+02 0.27477867E+00 0.1973008 0.1644084

0.10000000E+02 0.26669619E+00 0.2050367 0.1768951

0.10000000E+02 0.25861371E+00 0.2127726 0.1893818

0.10000000E+02 0.25053123E+00 0.2205085 0.2018685

0.10000000E+02 0.24244875E+00 0.2282444 0.2143553

0.10000000E+02 0.23436627E+00 0.2359803 0.2268420

0.10000000E+04 0.22628379E+00 0.2437162 0.2393287

VBANDEG.DAT (valence band structure)

strain lattice constant(quantum well)

-.117000E-01 0.593764E-09

width of each region material composition (x y) band offset (e.V)

0.10000000E+04 0.22628379E+00 0.2437162 -0.0930723

0.10000000E+02 0.23436627E+00 0.2359803 -0.0882163

0.10000000E+02 0.24244875E+00 0.2282444 -0.0833604

0.10000000E+02 0.25053123E+00 0.2205085 -0.0785044

0.10000000E+02 0.25861371E+00 0.2127726 -0.0736485

0.10000000E+02 0.26669619E+00 0.2050367 -0.0687925

0.10000000E+02 0.27477867E+00 0.1973008 -0.0639366

0.10000000E+02 0.28286115E+00 0.1895649 -0.0590807

0.10000000E+02 0.29094363E+00 0.1818290 -0.0542247

0.10000000E+02 0.29902611E+00 0.1740931 -0.0493688

0.10000000E+02 0.30710859E+00 0.1663572 -0.0445128

0.10000000E+03 0.14346182E+00 0.1576771 -0.0263168

0.10000000E+02 0.30710859E+00 0.1663572 -0.0445128

0.10000000E+02 0.29902611E+00 0.1740931 -0.0493688

0.10000000E+02 0.29094363E+00 0.1818290 -0.0542247

0.10000000E+02 0.28286115E+00 0.1895649 -0.0590807

0.10000000E+02 0.27477867E+00 0.1973008 -0.0639366

0.10000000E+02 0.26669619E+00 0.2050367 -0.0687925

0.10000000E+02 0.25861371E+00 0.2127726 -0.0736485

0.10000000E+02 0.25053123E+00 0.2205085 -0.0785044

0.10000000E+02 0.24244875E+00 0.2282444 -0.0833604

0.10000000E+02 0.23436627E+00 0.2359803 -0.0882163

0.10000000E+04 0.22628379E+00 0.2437162 -0.0930723

B.2. 1.55μm InGaAlAs/InGaAlAs compressive strained Multiple-Quantum-Well lasers ( 3 quantum wells ) with GRIN structure.

This example shows how to generate the CBANDEG.DAT and VBANDEG.DAT for a MQW laser with three quantum wells and GRIN structure. The design of a MQW laser consists of 6 steps. The first 5 steps are the same to that of the Single-quantum-well laser, and obtain two output files including the CBANDEG.DAT and the VBANDEG.DAT. The sixth step is to modify these two files and create new files for the MQW laser.

Step 1- Step 5: The same to the SQW case

CBANDEG.DAT(conduction band structure)

strain lattice constant(quantum well)

-.117000E-01 0.596875E-09

width of each region material composition (x y) band offset (e.V)

0.10000000E+04 0.22628379E+00 0.2437162 0.2393287

0.10000000E+02 0.23436627E+00 0.2359803 0.2268420

0.10000000E+02 0.24244875E+00 0.2282444 0.2143553

0.10000000E+02 0.25053123E+00 0.2205085 0.2018685

0.10000000E+02 0.25861371E+00 0.2127726 0.1893818

0.10000000E+02 0.26669619E+00 0.2050367 0.1768951

0.10000000E+02 0.27477867E+00 0.1973008 0.1644084

0.10000000E+02 0.28286115E+00 0.1895649 0.1519217

0.10000000E+02 0.29094363E+00 0.1818290 0.1394350

0.10000000E+02 0.29902611E+00 0.1740931 0.1269483

0.10000000E+02 0.30710859E+00 0.1663572 0.1144615

0.10000000E+03 0.14346182E+00 0.1576771 0.0526335

0.10000000E+02 0.30710859E+00 0.1663572 0.1144615

0.10000000E+02 0.29902611E+00 0.1740931 0.1269483

0.10000000E+02 0.29094363E+00 0.1818290 0.1394350

0.10000000E+02 0.28286115E+00 0.1895649 0.1519217

0.10000000E+02 0.27477867E+00 0.1973008 0.1644084

0.10000000E+02 0.26669619E+00 0.2050367 0.1768951

0.10000000E+02 0.25861371E+00 0.2127726 0.1893818

0.10000000E+02 0.25053123E+00 0.2205085 0.2018685

0.10000000E+02 0.24244875E+00 0.2282444 0.2143553

0.10000000E+02 0.23436627E+00 0.2359803 0.2268420

0.10000000E+04 0.22628379E+00 0.2437162 0.2393287

VBANDEG.DAT (valence band structure)

strain lattice constant(quantum well)

-.117000E-01 0.593764E-09

width of each region material composition (x y) band offset (e.V)

0.10000000E+04 0.22628379E+00 0.2437162 -0.0930723

0.10000000E+02 0.23436627E+00 0.2359803 -0.0882163

0.10000000E+02 0.24244875E+00 0.2282444 -0.0833604

0.10000000E+02 0.25053123E+00 0.2205085 -0.0785044

0.10000000E+02 0.25861371E+00 0.2127726 -0.0736485

0.10000000E+02 0.26669619E+00 0.2050367 -0.0687925

0.10000000E+02 0.27477867E+00 0.1973008 -0.0639366

0.10000000E+02 0.28286115E+00 0.1895649 -0.0590807

0.10000000E+02 0.29094363E+00 0.1818290 -0.0542247

0.10000000E+02 0.29902611E+00 0.1740931 -0.0493688

0.10000000E+02 0.30710859E+00 0.1663572 -0.0445128

0.10000000E+03 0.14346182E+00 0.1576771 -0.0263168

0.10000000E+02 0.30710859E+00 0.1663572 -0.0445128

0.10000000E+02 0.29902611E+00 0.1740931 -0.0493688

0.10000000E+02 0.29094363E+00 0.1818290 -0.0542247

0.10000000E+02 0.28286115E+00 0.1895649 -0.0590807

0.10000000E+02 0.27477867E+00 0.1973008 -0.0639366

0.10000000E+02 0.26669619E+00 0.2050367 -0.0687925

0.10000000E+02 0.25861371E+00 0.2127726 -0.0736485

0.10000000E+02 0.25053123E+00 0.2205085 -0.0785044

0.10000000E+02 0.24244875E+00 0.2282444 -0.0833604

0.10000000E+02 0.23436627E+00 0.2359803 -0.0882163

0.10000000E+04 0.22628379E+00 0.2437162 -0.0930723

Step 6: Modify the output files

This step is to modify both output files. Before modifying, either CBANDEG.DAT or VBANDEG.DAT file consists of one quantum well layer and SCH layers. Since we want to design a three-quantum-well laser, two more quantum well layers and two barrier layers should be added in each output file. The added quantum well layers are the same to the quantum well layer (12^th row) generated in the previous step. However, the added barrier layers should be generated manually. The barrier thickness is the 100Å shown in table I, and the barrier composition and the band offset are the same to the first row of the SCH layer or the 2^nd row in the CBANDEG.DAT/VBANDEG.DAT. Finally, four added layers are put in the 13-16 rows, and each barrier layer is inserted between two quantum well layers, which is indicated by the bold Italic in the final CBANDEG.DAT and VBANDEG.DAT.

CBANDEG.DAT(conduction band structure)

strain lattice constant(quantum well)

-.117000E-01 0.596875E-09

width of each region material composition (x y) band offset (e.V)

0.10000000E+04 0.22628379E+00 0.2437162 0.2393287

0.10000000E+02 0.23436627E+00 0.2359803 0.2268420

0.10000000E+02 0.24244875E+00 0.2282444 0.2143553

0.10000000E+02 0.25053123E+00 0.2205085 0.2018685

0.10000000E+02 0.25861371E+00 0.2127726 0.1893818

0.10000000E+02 0.26669619E+00 0.2050367 0.1768951

0.10000000E+02 0.27477867E+00 0.1973008 0.1644084

0.10000000E+02 0.28286115E+00 0.1895649 0.1519217

0.10000000E+02 0.29094363E+00 0.1818290 0.1394350

0.10000000E+02 0.29902611E+00 0.1740931 0.1269483

0.10000000E+02 0.30710859E+00 0.1663572 0.1144615

0.10000000E+03 0.14346182E+00 0.1576771 0.0526335 – 1^st QW

0.10000000E+03 0.23436627E+00 0.2359803 0.2268420 – 1^st BARRIER

0.10000000E+03 0.14346182E+00 0.1576771 0.0526335 – 2^nd QW

0.10000000E+03 0.23436627E+00 0.2359803 0.2268420 – 2^nd BARRIER

0.10000000E+03 0.14346182E+00 0.1576771 0.0526335 – 3^rd QW

0.10000000E+02 0.30710859E+00 0.1663572 0.1144615

0.10000000E+02 0.29902611E+00 0.1740931 0.1269483

0.10000000E+02 0.29094363E+00 0.1818290 0.1394350

0.10000000E+02 0.28286115E+00 0.1895649 0.1519217

0.10000000E+02 0.27477867E+00 0.1973008 0.1644084

0.10000000E+02 0.26669619E+00 0.2050367 0.1768951

0.10000000E+02 0.25861371E+00 0.2127726 0.1893818

0.10000000E+02 0.25053123E+00 0.2205085 0.2018685

0.10000000E+02 0.24244875E+00 0.2282444 0.2143553

0.10000000E+02 0.23436627E+00 0.2359803 0.2268420

0.10000000E+04 0.22628379E+00 0.2437162 0.2393287

VBANDEG.DAT (valence band structure)

strain lattice constant(quantum well)

-.117000E-01 0.593764E-09

width of each region material composition (x y) band offset (e.V)

0.10000000E+04 0.22628379E+00 0.2437162 -0.0930723

0.10000000E+02 0.23436627E+00 0.2359803 -0.0882163

0.10000000E+02 0.24244875E+00 0.2282444 -0.0833604

0.10000000E+02 0.25053123E+00 0.2205085 -0.0785044

0.10000000E+02 0.25861371E+00 0.2127726 -0.0736485

0.10000000E+02 0.26669619E+00 0.2050367 -0.0687925

0.10000000E+02 0.27477867E+00 0.1973008 -0.0639366

0.10000000E+02 0.28286115E+00 0.1895649 -0.0590807

0.10000000E+02 0.29094363E+00 0.1818290 -0.0542247

0.10000000E+02 0.29902611E+00 0.1740931 -0.0493688

0.10000000E+02 0.30710859E+00 0.1663572 -0.0445128

0.10000000E+03 0.14346182E+00 0.1576771 -0.0263168 – 1^st QW

0.10000000E+03 0.23436627E+00 0.2359803 -0.0882163 – 1^st BARRIER

0.10000000E+03 0.14346182E+00 0.1576771 -0.0263168 – 2^nd QW

0.10000000E+03 0.23436627E+00 0.2359803 -0.0882163 – 2^nd BARRIER

0.10000000E+03 0.14346182E+00 0.1576771 -0.0263168 – 3^rd QW

0.10000000E+02 0.30710859E+00 0.1663572 -0.0445128

0.10000000E+02 0.29902611E+00 0.1740931 -0.0493688

0.10000000E+02 0.29094363E+00 0.1818290 -0.0542247

0.10000000E+02 0.28286115E+00 0.1895649 -0.0590807

0.10000000E+02 0.27477867E+00 0.1973008 -0.0639366

0.10000000E+02 0.26669619E+00 0.2050367 -0.0687925

0.10000000E+02 0.25861371E+00 0.2127726 -0.0736485

0.10000000E+02 0.25053123E+00 0.2205085 -0.0785044

0.10000000E+02 0.24244875E+00 0.2282444 -0.0833604

0.10000000E+02 0.23436627E+00 0.2359803 -0.0882163

0.10000000E+04 0.22628379E+00 0.2437162 -0.0930723

Chapter 1 Introduction

I) # For GRIN STRUCTURE (STEP) N=:

II) WELL, BARRIER AND CLADDING WAVELENGTH:

III) CLADDING, BARRIER, and QUANTUM WELL WIDTH:

IV) INPUT STRAIN:

2.2 Output Parameters

CBANDEG.DAT (conduction band structure)

VBANDEG.DAT (valence band str ucture)

ENERGY EIGENVALUE ===> 0.483243413318E+00 ERROR= .2481610E-14

INPUT THE NAME OF OUTPUT FILE

Chapter 4 Simulations of Gain and Laser Properties

4.1 Theories for computations of Gain and Important Laser Properties

4.1.1 Gain Calculations

4.1.2 Threshold Current Density (Jth) and Slope Efficiency Calculations

4.1.2.1 Threshold Current Density (Jth) Calculations:

4.1.2.2 L-I Curve and Slope Efficiency Calculations

4.4 Running the Software for Gain and Laser Characteristics

9 InzGa1-zAs/AlxGayIn1-x-yAs/AlxGayIn1-x-yAs(Substrate: InP)

B.1 A 1.55μm InGaAlAs/InP compressive strained Single-Quantum-Well laser with GRIN structure

B.2. 1.55μm InGaAlAs/InGaAlAs compressive strained Multiple-Quantum-Well lasers ( 3 quantum wells ) with GRIN structure.