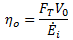
Problem Statement:
A small propeller-driven airplane is flying at a speed where its total drag is 1250 N. The aircraft engine is burning 0.44 L/min (4.4 x 10-4 m3/min) of fuel. The fuel has a density of 700 kg/m3 and an energy density of 43.5 MJ/kg. The thermal efficiency of the engine is ηth = 25% and the propulsive efficiency of the propeller is ηp = 80%. How fast is the airplane flying?
Solution:
From the definition of overall efficiency we have
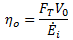
But for steady flight, FT = FD. Also, we know that ηo = ηthηp. Substituting all of this into the above equation and solving for the airplane speed gives
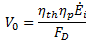
All we need to know is how to find the energy input. The energy input comes from the chemical energy in the fuel and is computed as
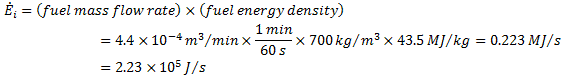
Thus, we compute the airplane speed as

or, about 80 mph. Note that we have used the fact that 1 J = 1 N m/s in the calculation.
