Biol/Chem 5310

Lecture:4

September 3, 2002

Thermodynamics

The science of energy transformation

  • In principle, thermodynamics will allow us to predict whether a process is favorable or not. (However, it will not indicate the rate at which a reaction will proceed.)
  • An understanding of thermodynamics may help us to predict things such as the 3-dimensional structure of proteins.

    • The System

  • Everything that is within specified boundaries
  • e.g. the universe, this room, my cup
  • It can be closed or open to exchange of heat or matter.
  • Living systems are always open.
  • The state of a system is specified by 2 of 3 variables:
  • P-pressure, T-temperature, or V-volume
  • and the number (ni) or mass (gi) of each component i
  • This is like a recipe.

    • Internal Energy (U)

  • U is a state function of a system.
  • In a chemical context it includes:
  • kinetic energy of motion
  • vibrational energy
  • rotational energy
  • chemical bond energy
  • When the system changes, the new state will specify a new internal energy, U2
  • DU = U2 - U1
  • U2 will not depend upon the process, or pathway of the transformation, but only on the P,V,T etc of the new state.
  • Such processes include
  • exchange of heat with surroundings
  • work done by system on surroundings
  • Heat (q) and Work (w) are not state functions

    • First Law of Thermodynamics (conservation of energy)

  • DU = q - w
  • In biochemical systems, P is generally constant.
  • If work is only of the PdV type
  • DU = q - PDV
  • q = DU + PDV
  • In this case the heat exchanged is not DU

    • Enthalpy

  • A new state function can be defined as H such that under these conditions q = DH
  • H is called enthalpy
  • H = U + PV
  • DH = DU + PDV + VDP
  • at constant P, DH = DU + PDV

    • The heat of a reaction is equal to the change in a state function under these conditions:

  • At constant volume, q = DU
  • At constant pressure, q= DH
  • In biochemistry, DH is usually about equal to DU

    • Is DH always an indicator of a favorable, or spontaneous reaction?

  • Not always, some reactions proceed with DH > 0 (heat absorbed)
  • Is there another state function that is predictive of favorable processes in biochemical systems?
  •  
  •  

    •   Ludwig Boltzmann (visit the link, courtesy of U. of St. Andrews, Scotland)

    First, consider another kind of process

  • A sucrose solution with water layered carefully on top: now 2 layers
  • Eventually, via diffusion, the sucrose will occupy the upper layer also.
  • This process is characterized by a more ordered state changing to a less ordered state.
  • This randomness can be characterized by a state function defined by Boltzmann as entropy, S.

    • S = kB ln W

  • kB is the Boltzmann constant (It is equal to R, the gas constant divided by Avogadro's number) See Box 1-1, p. 14.
  • On a per mole basis use R: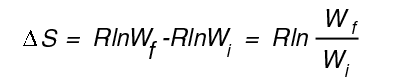
  • Here W refers to the number of ways of distributing the sucrose molecules in the solution.
  • Since W is proportional to the volume, if the volume doubles, DS = Rln2
  • ln2 = .69
  • R= 8.31 J K-1 mol-1

    • Second Law of Thermodynamics

  • "The entropy of an closed system will tend to increase to a maximum value."
  • Energetically, there is nothing that disfavors the gathering of sucrose in a corner.
  • So, entropy must play a part in determining whether a process is favorable or spontaneous.
  •  
  •  

          Josiah Willard Gibbs  (visit the link, courtesy of U. of St. Andrews, Scotland)

    G, a new state function

  • We need another state function that incorporates the predictive powers of DH and DS.
  • Gibbs defined such a function as G = H - TS
  • DG = DH -TDS - SDT
  • At constant T (and P)
  • DG = DH -TDS
  • If DG < 0, a process is favorable.
  • In a closed system, DH = 0 , so a favorable process must be entropy-driven

    • How to Apply G to chemical equilibrium

  • Gsystem = G1 + G2 + ...
  • Each Gi = NiGi
  • where for each component i, Ni is number of moles, and Gi is the partial molar free energy (chemical potential)
  • Gi = Gi° + RTln[ci]

    • Consider a reaction: aA + bB <=> cC + dD

  • What is DG for converting a moles of A and b moles of B into c moles of C and d moles of D?
  • where
  • So DG is equal to the sum of two terms:
  • A DG term for conversion under standard state conditions of 1 M  ()
  • And a term for DG° that depends on the actual concentrations of each species.( )

    •          

  • At equilibrium, DG = 0 , so the two terms on the right must cancel.
  • This leads to an expression relating the standard state DG° to the equilibrium constant.
  • DG° = - RT ln Keq
  • Knowledge of DG° is equivalent to knowledge of Keq
  • The exponential relationship means that small changes in DG lead to large changes in Keq
  • each 5.7 kJ/mol or 1.4 kcal/mol indicates a 10x change in K

    Example to be solved: Glucose-6-Phosphate <=> Fructose-6-phosphate, DG°= 1.7 kJ/mol

  • What is the Keq ?
  • What are the concentrations of each at equilibrium if we start with 5 mM Glucose-6-phosphate?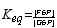
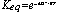
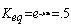
  •         or [G6P] = 2[F6P]
  • We can calculate the percentage of each in solution at equilibrium, or if we know the total concentration, we can calculate the concentration of each.
  • [F] + [G] = 100
    [F] +2[F] = 100
    [F] = 33%
    [G] = 67%
  • or
  • if total concentration is 5 mM,
  • [F] + [G] = 5

    • In living systems many essential reactions are unfavorable

  • e.g. synthesis of proteins
  • How are such reactions driven?
  • Sometimes by coupling to a favorable reaction e.g. hydrolysis of ATP

    • ATP is an example of a meta-stable species

  • It exists in living cells at mM conc.
  • Its hydrolysis is highly favored
  • Its uncatalyzed rate of hydrolysis is very slow
  • It is trapped kinetically until it encounters an enzyme that uses it.

    • Try a quiz in Ch. 1

    Comments/questions: svik@mail.smu.edu

    Copyright 2002, Steven B. Vik, Southern Methodist University