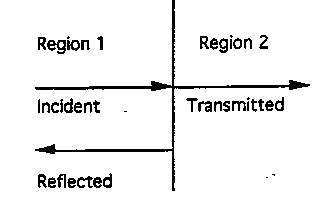
1. In the figure below, light with a wavelength of 0.98 µm is incident (perpendicular to the interface) from Region 1 with n1 = 1.45, into Region 2 with n2 = 1.57 ELECTRICAL ENGINEERING DEPARTMENT
SOUTHERN METHODIST UNIVERSITY
FIBER OPTIC TELECOMMUNICATIONS
SMU EE 5303 NTU TM-513-N Midterm #2 April 13-18, 1997
Name (print): ________________________
Location: ________________________
Date and Time Exam taken: ________________________
Note #1: please indicate your location: (NTU, TAGER, Video Distance, Video on Campus, or Campus-live) and the date and time of the exam above
Note #2: some of the multiple choice questions may have more than one correct answer listed. If so, circle all of the correct responses for the question.
Note #3: please print your name at the bottom of the remaining pages.
Note #4: please provide a brief explanation of your answers to multiple-choice type questions.
Note #5: several figures are shown on the last pages that could be helpful in solving some of the problems below.
Note #6: each question is worth 5 points.
TIME: The allowed time period is 120 minutes.
CONSTRAINTS: This exam is closed to books and notes with the exception below:
ALLOWED: 2 page of notes (81/2 x 11; can write on both sides); calculator; straight edge; ruler; and compass.
NOTE TO SITE COORDINATORS AND/OR PROCTORS:
THIS EXAM CONTAINS 17 PAGES AND 20 PROBLEMS--make sure all the pages are included.
IF THIS EXAM WAS FAXED TO YOU
, make sure that each page is readable. There should be a minimum margin of one-half inch on all four sides. If this is not the case, please call Shirley Braun and request that the exam be sent again.
YOUR SIGNATURE IS REQUIRED ON PAGE 11
1. In the figure below, light with a wavelength of 0.98 µm is incident (perpendicular to the interface) from Region 1 with n1 = 1.45, into Region 2 with n2 = 1.57
i) Find the fraction of light reflected back into Region 1.
ii) Find the fraction of light transmitted into Region 2.
iii) What would your answers be if the light was incident from Region 2 into Region 1?
2. i) write down the equation for pulse spreading per unit length due to material dispersion:
ii) write down the equation for pulse spreading per unit length due to waveguide dispersion:
iii) write down the equation for multimode distortion:
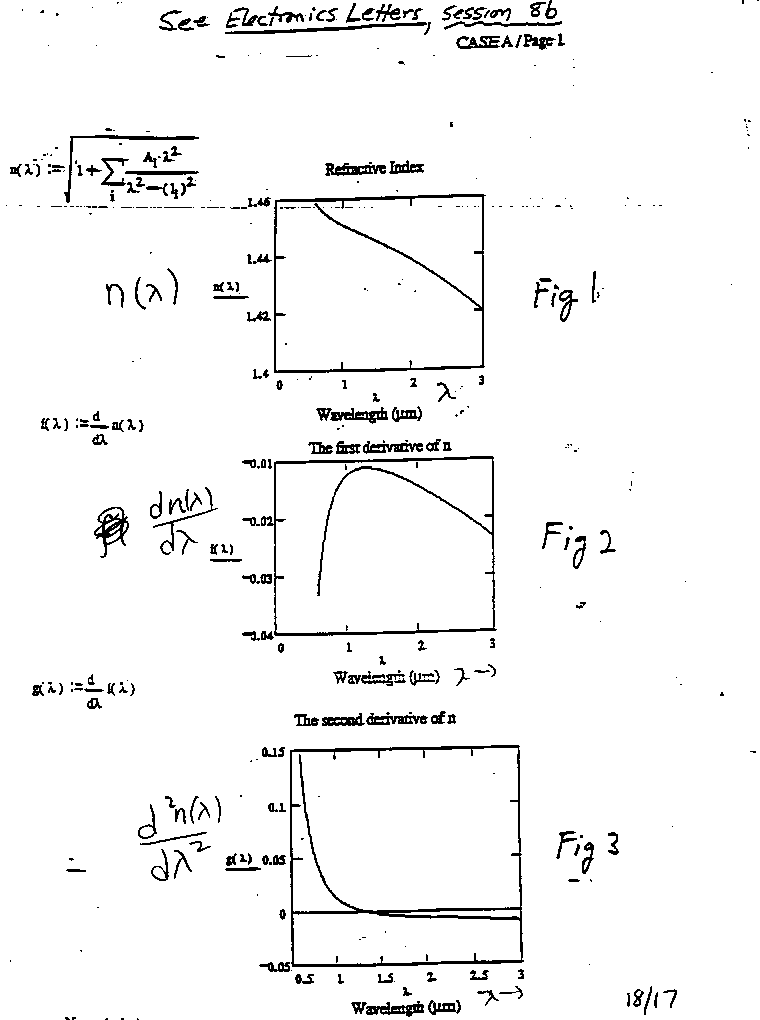
3. The index of refraction in an optically transparent material is given by:
n(
a) what is the index of refraction of this material at a wavelength of 1.0 µm?
b) what is the phase velocity of an optical wave propagating in this material if the wavelength of the light is 1.0 µm?
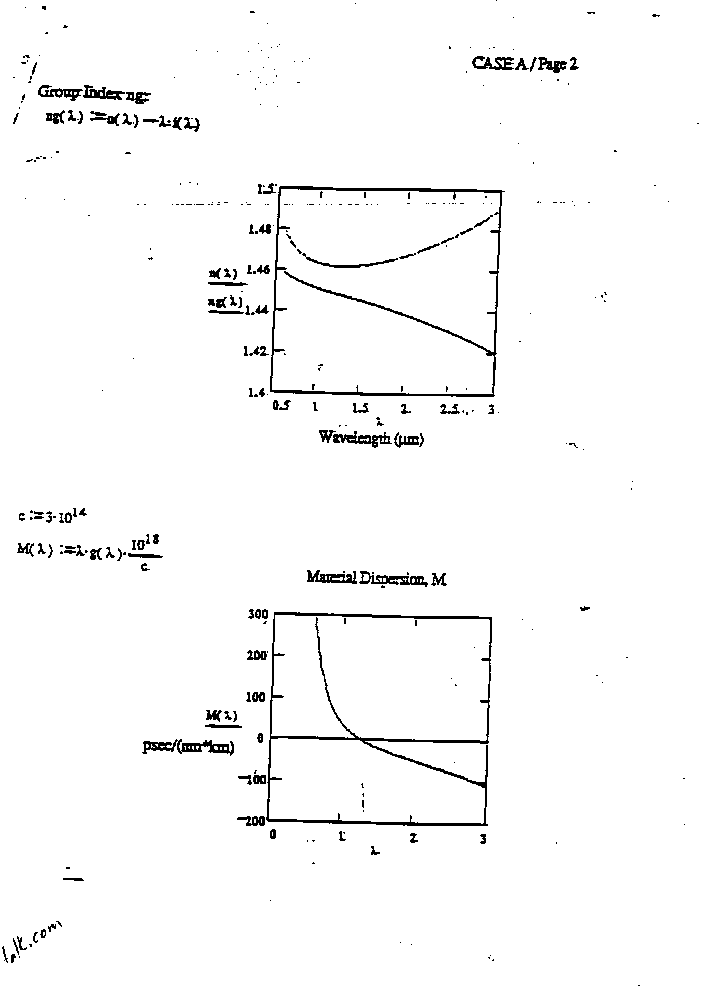
4. For the same optically transparent material described in problem 3, what is the group index for optical waves with wavelengths between 0.7 µm and 3.0 µm?
5. For the same optically transparent material described in problem 3, calculate the pulse spreading if an optical pulse with a wavelength of 2.0 µm and a bandwidth
Dl = 20 nm travels a distance of 10 km.
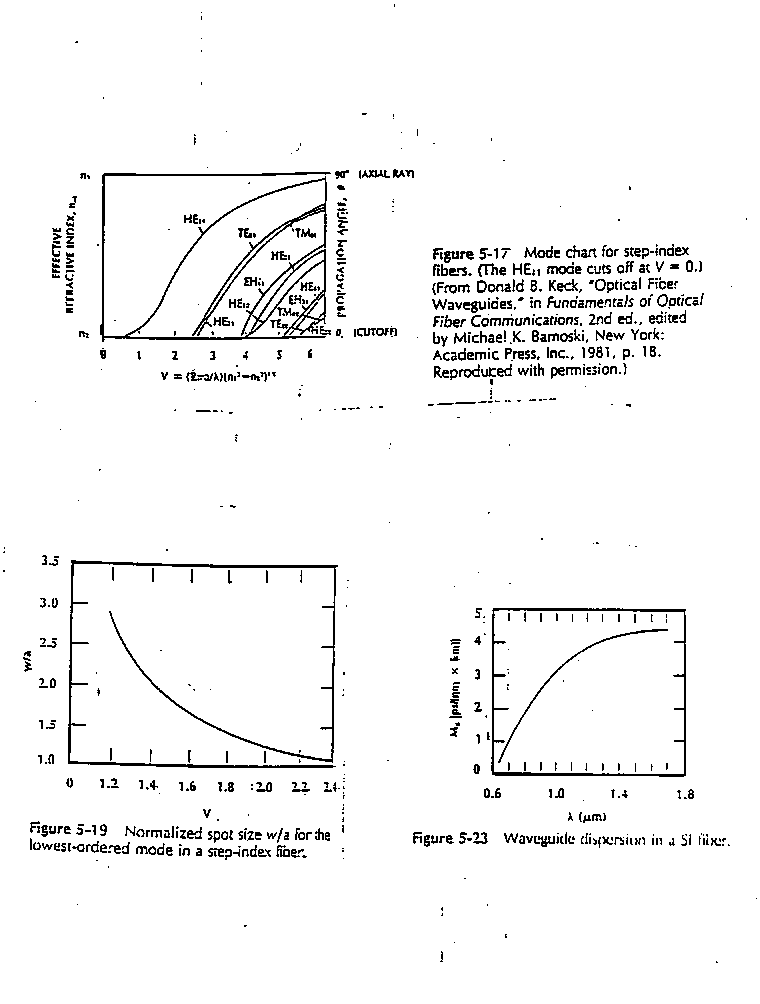
6. A SI fiber has core refractive index of n1 = 1.655, and a cladding index of
n2 = 1.650. The normalized frequency V is 2.1 If the source wavelength is
l = 1.55 µm:
a) what is the core radius of this fiber?
b) what is the numerical aperture (NA) of this fiber?
c) what is the spot-size of this fiber?
d) how many modes can propagate in this fiber? Briefly explain your answers.
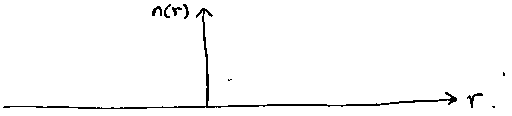7. i) Sketch the refractive index profile of a step-index (SI) fiber:
ii) Sketch the ray trajectories inside a step-index fiber. The open box below represents the core of the step-index fiber and the region outside the core represents the cladding region.
iii) Sketch the refractive index profile of a graded-index (GRIN) fiber:
.
iv) Sketch the ray trajectories inside a GRIN fiber. The open box below represents the core of the GRIN fiber and the region outside the core represents the cladding region.
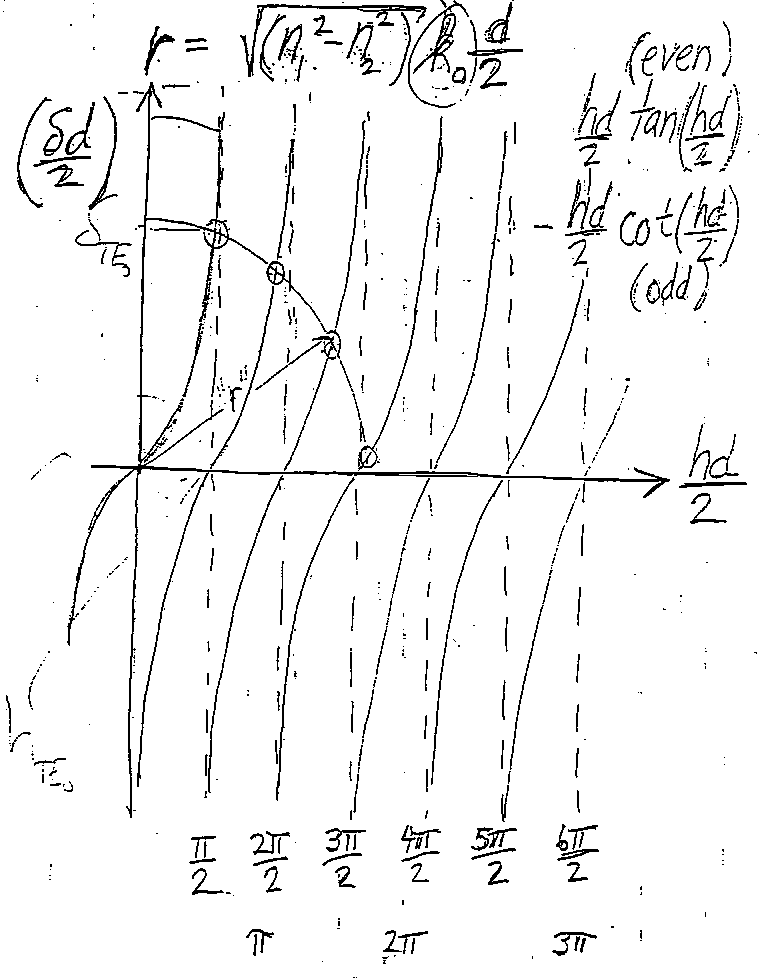
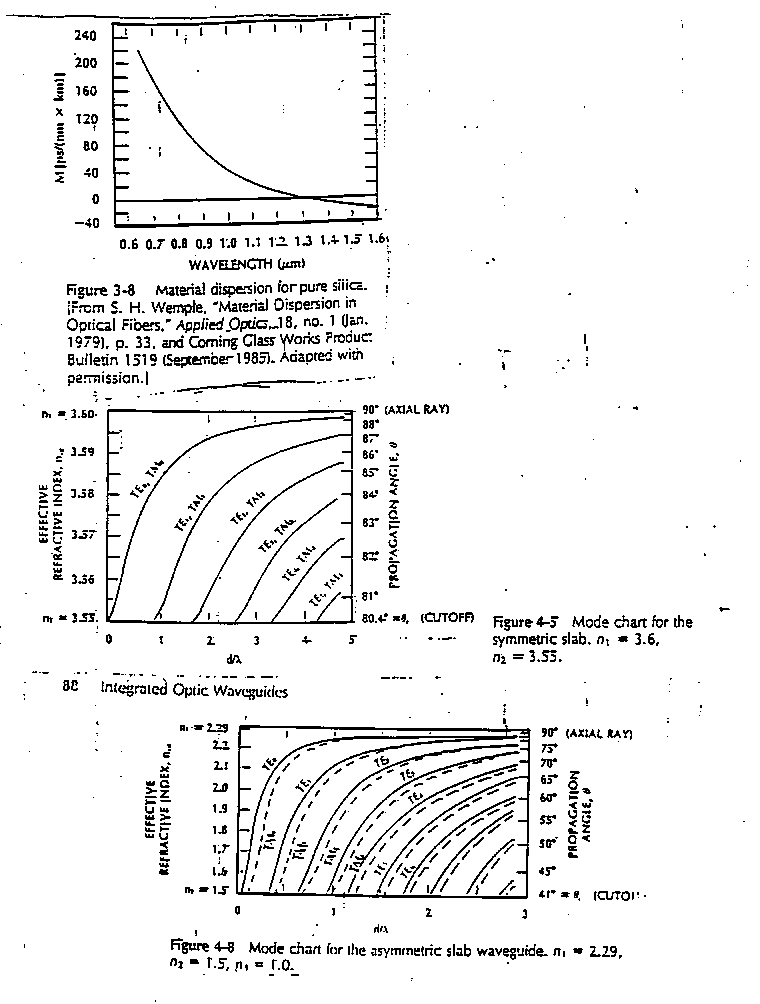
8. a) identify the following TM mode numbers of an asymmetric slab waveguide; b) indicate which distributions are intensity distributions and which are field distributions
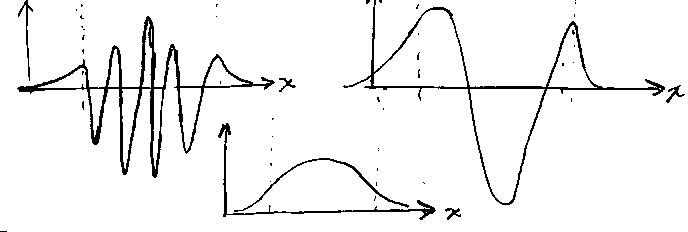
For problems 9 through 11 consider the five curves (attached at the end) that correspond to quenched SiO2 (Case A) that were plotted from equations in the Electronics Letters paper.
9. At what peak wavelength will a pulse propagating in quenched SiO2 have zero dispersion? Indicate the wavelength on the appropriate graph and give a numerical value for the wavelength.
10. i) As the peak wavelength of a pulse in quenched SiO2 is shifted away from the zero dispersion wavelength, what happens to the velocity of the pulse? (does it increase or decrease or what? why?)
ii) Give a physical explanation for your answer in part i).
11. Find the contribution to pulse spreading in a step index fiber (n1 = 1. 655 and n2 = 1.555, V = 2.2) which is due to material dispersion if the optical source is a laser operating at a free space wavelength of 1.55 µm. The laser has a spectral emission width of 2 nm. The length of the silica fiber is 20 km. The fiber is made from quenched SiO2.
12. Consider the step index fiber (n1 = 1. 655 and n2 = 1.555, V = 2.2) in problem 11.
a) find the amount of pulse spreading in the fiber due only to waveguide dispersion. The optical source is a laser operating at a free space wavelength of 1.55 µm. The laser has a spectral emission width of 2 nm. The length of the silica fiber is 20 km. The fiber is made from quenched SiO2.
b) what is the total (material and waveguide) dispersion for this fiber?
c) what is the 3-dB optical bandwidth of this fiber?
13. A step-index fiber with the same core and cladding index (n1 = 1. 655 and n2 = 1.555) as that used in problems 11 and 12 has a V number of 30.
a) what is the basic pulse spread per unit length due only to energy being distributed among multiple modes for this fiber? As in the previous problems, the optical source is a laser operating at a free space wavelength of 1.55 µm. The laser has a spectral emission width of 2 nm. The length of the silica fiber is 20 km. The fiber is made from quenched SiO2.
b) what is the total pulse spread due to multimode distortion over 20 km of this fiber if the equilibrium length of the fiber is 2 km? As in the previous problems, the optical source is a laser operating at a free space wavelength of 1.55 µm. The laser has a spectral emission width of 2 nm. The length of the silica fiber is 20 km. The fiber is made from quenched SiO2.
c) what is the 3-dB optical bandwidth of this fiber?
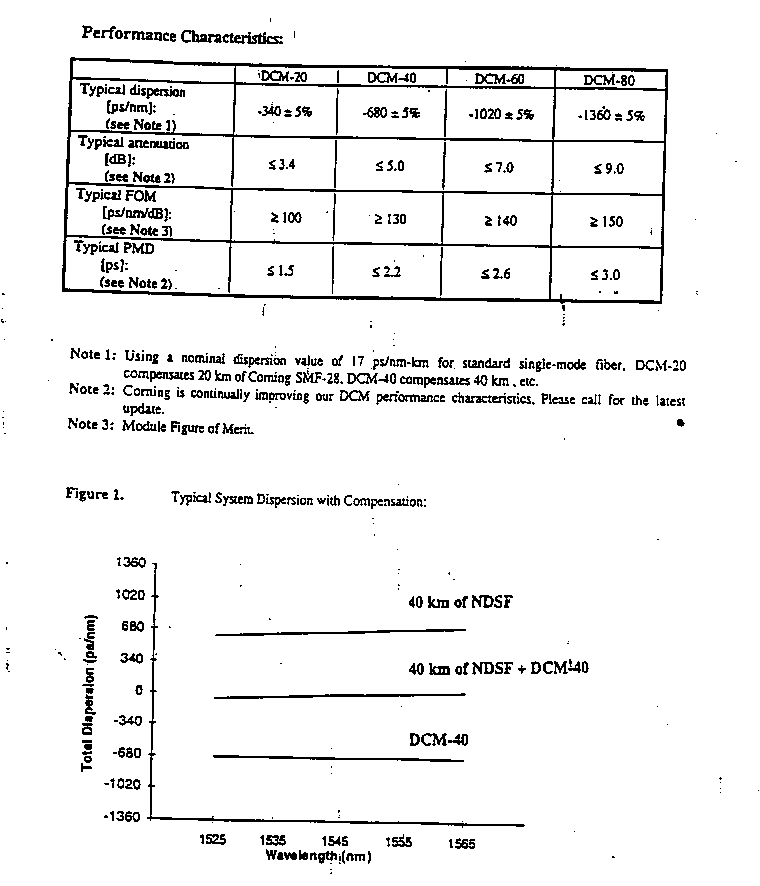
14. Consider the data sheet for Corning’s Dispersion Compensator Module.
a) can this module (or one of a similar design) be used to counteract the pulse spreading encountered in problems 11 and 12 (n1 = 1. 655 and n2 = 1.555, V = 2.2)?
b) can this module (or one of a similar design) be used to counteract the pulse spreading encountered in problem 13 (n1 = 1. 655 and n2 = 1.555, V = V = 30)?
15. Briefly discuss dispersion-shifted and dispersion-flattened fibers. Indicate a possible index profile for each type.
16. Which of the following waveguides can be designed so that no optical mode can propagate? Another way to ask this question is which waveguides can be designed to have all modes below cut-off? (Assume a finite, non-zero slab or core thickness and that the core or inner region has a higher index than the cladding regions.)
a) symmetric slab waveguides
b) step-index circular fiber waveguides
c) asymmetric slab waveguides
17. Consider a symmetric slab waveguide (or a circular step-index fiber waveguide). If all parameters are held constant except the index of the cladding decreases, will the number of propagating modes increase or decrease? Briefly explain.
18. Consider a symmetric slab waveguide (or a circular step-index fiber waveguide). If all parameters are held constant except the index of the core increases, will the fraction of the energy (of the fundamental propagating mode) in the cladding regions increase, decrease, or remain the same? Briefly explain.
19. Approximately how many modes will an optical fiber with a core diameter of 100 µm and a cladding diameter of 200 µm support if the core index is 1.48 and the cladding index is 1.47? The light propagating in this fiber has a wavelength of 1.32 µm.
20. For a single-mode step-index fiber, what are the limits on the V parameter? What determines these limits?
CERTIFICATION OF TESTING ENVIRONMENT:
I certify that I have completed this test in the 90 minute time period allotted, and that I have neither given nor received help from another person, nor have I had advanced access to questions or answers.
Signed:________________________date:________
SITE COORDINATORS AND/OR PROCTORS:
I distributed and collected this test in a 120 minute interval
on_______________________________(date).
Signed__________________________________
Site Coordinator/Proctor must sign
