1) Problem 14 on page 93 of the textbook
Let Xij be the number of liters of input i used to make product j where
the inputs and products are numbered as shown below:
|
One liter of regular gasoline sells for 29.49 cents,
but it costs (1.5)(8.5) cents to remove the lead from it. Thus, a liter
of regular gasoline a net value of 16.74 cents. Likewise, a liter of premium
gasoline has a net value of 16.68 cents.
Thus, the objective function is:
maximize 16.74 x11 + 18.68 x12 + 16.74 x21 + 18.68 x22 + 16.74 x31
+ 18.68 x32 + 16.74 x41 + 18.68 x42 + 16.74 x51 + 18.68 x52
+ 16.74 x61 + 18.68 x62
The constraints are:
FCG limit1: - 0.38 x11 + 0.62 x21 - 0.38 x31 - 0.38 x41 - 0.38 x51 - 0.38 x61 <= 0
FCG limit2: - 0.38 x12 + 0.62 x22 - 0.38 x32 - 0.38 x42 - 0.38 x52- 0.38 x62 <= 0
availability1: x11 + x12 <= 15572
availability2: x21 + x22 <= 15434
availability3: x31 + x32 <= 6709
availability4: x41 + x42 <= 1190
availability5: x51 + x52 <= 748
meet demand regular: x11 + x21 + x31 + x41 + x51 + x61 >= 9800
meet demand perimum: x12 + x22 + x32 + x42 + x52 + x62 >= 30000
regular ron: 8.9 x11 + 3.2 x21 - 3.9 x31 + 7 x41 + 27 x51 + 8 x61 >= 0
premium ron: 2.9 x12 - 2.8 x22 - 9.9 x32 + x42 + 21 x52 + 2 x62 >= 0
rvp requirement1: - 13.52 x11 - 11.4 x21 + 8.34 x31 - 6.67 x41 -7.73 x51 + 145.81 x61 = 0
rvp requirement2: - 13.52 x12 - 11.4 x22 + 8.34 x32 - 6.67 x42 -7.73 x52+ 145.81 x62 = 0
astm70 requirement1: - 15 x11 + 47 x21 + 97 x31 - 3 x41 + 88 x51 + 120 x61 >= 0
astm70 requirement2: - 15 x12 + 47 x22 + 97 x32 - 3 x42 + 88 x52 + 120 x62 >= 0
astm130 requirement1: - 4 x11 + 53 x21 + 50 x31 - 43 x41 + 50 x51 + 50 x61 >= 0
astm130 requirement2: - 4 x12 + 53 x22 + 50 x32 - 43 x42 + 50 x52 + 50 x62 >= 0
xij >= 0 for all i and j
Here is the solution from CPLEX;
Primal - Optimal: Objective = 7.6580822735e+05
Solution time = 0.00 sec. Iterations = 11 (9)
| Variable Name | Solution Value |
| x11 | 1265.859769 |
| x12 | 14306.140231 |
| x21 | 3192.706296 |
| x22 | 12241.293704 |
| x31 | 3956.295964 |
| x32 | 2752.704036 |
| x41 | 1190.000000 |
| x52 | 748.000000 |
| x61 | 195.137971 |
| x62 | 2165.792830 |
All other variables in the range 1-12 are zero.
2) Problem 11 on page 98
Let PA be the number of pounds of product A produced.
Let PB be the number of pounds of product B produced.
Note that this includes pounds of B produced directly from the raw material and from product A.
Let PC be the number of pounds of product C produced.
Let ABC be the number of pounds of product A converted to products B and C by the process that costs $3. Note that one lb of ABC yields 0.6 lbs of product B and 0.4 lbs of product C.
Let BC be the number of pounds of product B converted to product C by the process that costs $2. Note that one lb of BC yields 0.8 lbs of product C.
Let SA, SB and SC be the amount (in lbs) of products A, B and C sold respectively.
A valid LP formulation is:
| maximize revenue -cost | (net profit) |
| subject to | |
| cost = 5 * (PA + PB) +3* ABC + 2 * BC | |
| revenue = 10 * SA + 12 * SB + 20 * SC | |
| SA <= PA - ABC | (Can't sell more A than is produced) |
| SB <= PB + 0.6 * ABC - BC | (Can't sell more B than is produced) |
| PC = 0.4 * ABC + 0.8 * BC | (lbs of C produced) |
| SC <= PC | (Can't sell more C than is produced) |
| SA <= 30 | (Maximum lbs of A that can be sold) |
| SB <= 30 | (Maximum lbs of B that can be sold) |
| SC <= 30 | (Maximum lbs of C that can be sold) |
| All variables >= 0 |
An optimal solution is show below.
SA = 30
SB = 30
SC = 30
PA = 30
PB = 67.5
PC = 30
ABC = 0
BC = 37.5
revenue - cost = $697.5
3) #5 on Page 104
Let Ti be the number of trucks produce in month i.
Let Ci be the number of cars produced in month i.
Let ITi be the of trucks in inventory at the end
of month i.
Let CTi be the number of cars inventory at the end
of month i.
Let Si be the tons of steel used in month i
The objective function has two components: the cost of steel and the holding cost.
Min 400 S1 + 600 S2 + 150 (IT1 + IT2 + IC1 + IC2)
The first set of constraints are standard inventory balance constraints which say that the inventory of a product at the end of a period is the amount produced in the period plus the inventory from the previous period minus the demand during the period.
IT1 = T1 + 100 - 400
IT2 = T2 + IT1 - 300
IC1 = C1 + 200 - 800
IC2 = C2 + IC1 - 300
Since we require all variables to be non-negative, we ensure that the demand is met every period. Next, we have constraints on the number of vehicles that can be produced each month.
T1 + C1 <= 1000
T2 + C2 <= 1000
Next, we have a set of constraints on the amount of steel used.
S1 >= 2 T1 + C1
S2 >= 2 T2 + C2
S1 <= 1500
S2 <= 1500
Finally , we the constraints enforcing the minimum mpg average.
(10 T1 + 20 C1) / (T1 + C1) >= 16 -> 4 C1 - 6 T1 >= 0
(10 T2 + 20 C2) / (T2 + C2) >= 16 -> 4 C2 - 6 T2 >= 0
Here is a CPLEX formulation of the problem:
Log started (V6.5.3) Sun Oct 1 14:02:27 2000
Problem 'cartruck.lp' read.
Read time = 0.00 sec.
Minimize
obj: 400 S1 + 600 S2 + 150 IT1 + 150 IT2 + 150 IC1 + 150 IC2
Subject To
c1: IT1 - T1 = -300
c2: - IT1 + IT2 - T2 = -300
c3: IC1 - C1 = -600
c4: - IC1 + IC2 - C2 = -300
c5: T1 + C1 <= 1000
c6: T2 + C2 <= 1000
c7: S1 - 2 T1 - C1 >= 0
c8: S2 - 2 T2 - C2 >= 0
c9: S1 <= 1500
c10: S2 <= 1500
c11: - 6 T1 + 4 C1 >= 0
c12: - 6 T2 + 4 C2 >= 0
Bounds
All variables are >= 0.
Tried aggregator 1 time.
LP Presolve eliminated 2 rows and 0 columns.
Aggregator did 2 substitutions.
Reduced LP has 8 rows, 8 columns, and 20 nonzeros.
Presolve time = 0.00 sec.
Iteration log . . .
Iteration: 1 Infeasibility = 2100.000000
Switched to devex.
Primal - Optimal: Objective = 9.9500000000e+05
Solution time = 0.00 sec. Iterations = 5 (5)
| Variable Name | Solution Value |
| S1 | 1400.000000 |
| S2 | 700.000000 |
| IT1 | 100.000000 |
| IC1 | 0.000000 |
| T1 | 400.000000 |
| T2 | 200.000000 |
| C1 | 600.000000 |
| C2 | 300.000000 |
All other variables in the range 1-10 are zero.
Thus, an optimal solution is produce 400 trucks and 600 cars in month 1 and 300 trucks and 200 cars in month 2.
3) Problem 4 on page 111 of the textbook.
Let St be the number of bushels of wheat sold during month t.
Let Bt be the number of bushels of wheat bought during month t.
Let It be the number of bushels of wheat in inventory
at the end of month t (after all buying and selling) during month t.
- PPt Bt
Let Pt be the profit in dollars for month t.
Denote by SPt and PPt the selling and buying price respectively in dollars per bushel for month t. For example, SP1 = 3 and PP1 = 8.
A correct formulation is
maximize P1 + P2 + P3
+ P4 + P5 + P6 + P7 + P8
+ P9 + P10
s.t.
| I0 = 6000 | ||
| It = It-1 + Bt - St | for t = 1,2,...,10 | Inventory Balance |
| It <= 20,000 | for t = 1,2,...,10 | Maximum Storage Capacity |
| St <= It-1 | for t = 1,2,...,10 | Can't sell more than is availalbe |
| Pt = SPt St - PPt Bt | for t = 1,2,...,10 | Definition of profit. |
The Pt are unrestricted in sign. All other variables are non-negative.
CPLEX Solution
Problem 'warehouse.lp' read.
Read time = 0.00 sec.
Maximize
obj: P0 + P1 + P2 + P3 + P4 + P5 + P6 + P7 + P8 + P9 + P10
Subject To
init_inventory: I0 = 6000
inventory1: - I0 + S1 - B1 + I1 = 0
inventory2: - I1 + S2 - B2 + I2 = 0
inventory3: - I2 + S3 - B3 + I3 = 0
inventory4: - I3 + S4 - B4 + I4 = 0
inventory5: - I4 + S5 - B5 + I5 = 0
inventory6: - I5 + S6 - B6 + I6 = 0
inventory7: - I6 + S7 - B7 + I7 = 0
inventory8: - I7 + S8 - B8 + I8 = 0
inventory9: - I8 + S9 - B9 + I9 = 0
inventory10: - I9 + S10 - B10 + I10 = 0
capacity0: I0 <= 20000
capacity1: I1 <= 20000
capacity2: I2 <= 20000
capacity3: I3 <= 20000
capacity4: I4 <= 20000
capacity5: I5 <= 20000
capacity6: I6 <= 20000
capacity7: I7 <= 20000
capacity8: I8 <= 20000
capacity9: I9 <= 20000
capacity10: I10 <= 20000
availiblity1: - I0 + S1 <= 0
availiblity2: - I1 + S2 <= 0
availiblity3: - I2 + S3 <= 0
availiblity4: - I3 + S4 <= 0
availiblity5: - I4 + S5 <= 0
availiblity6: - I5 + S6 <= 0
availiblity7: - I6 + S7 <= 0
availiblity8: - I7 + S8 <= 0
availiblity9: - I8 + S9 <= 0
availiblity10: - I9 + S10 <= 0
profit0: P0 = 0
profit1: P1 - 3 S1 + 8 B1 = 0
profit2: P2 - 6 S2 + 8 B2 = 0
profit3: P3 - 7 S3 + 2 B3 = 0
profit4: P4 - S4 + 3 B4 = 0
profit5: P5 - 4 S5 + 4 B5 = 0
profit6: P6 - 5 S6 + 3 B6 = 0
profit7: P7 - 5 S7 + 3 B7 = 0
profit8: P8 - S8 + 2 B8 = 0
profit9: P9 - 3 S9 + 5 B9 = 0
profit10: P10 - 2 S10 + 5 B10 = 0
Bounds
All variables are >= 0.
Tried aggregator 1 time.
LP Presolve eliminated 17 rows and 9 columns.
Aggregator did 14 substitutions.
Reduced LP has 12 rows, 19 columns, and 42 nonzeros.
Presolve time = 0.00 sec.
Iteration log . . .
Iteration: 1 Scaled infeas = 0.000000
Switched to devex.
Iteration: 2 Objective = 42000.000000
Primal - Optimal: Objective = 1.4200000000e+05
Solution time = 0.00 sec. Iterations = 10 (1)
| VariableName | SolutionValue |
| P3 | 2000.000000 |
| P6 | 40000.000000 |
| P7 | 100000.000000 |
| I0 | 6000.000000 |
| I1 | 6000.000000 |
| I2 | 6000.000000 |
| S3 | 6000.000000 |
| B3 | 20000.000000 |
| I3 | 20000.000000 |
| I4 | 20000.000000 |
| S5 | 20000.000000 |
| B5 | 20000.000000 |
| I5 | 20000.000000 |
| S6 | 20000.000000 |
| B6 | 20000.000000 |
| I6 | 20000.000000 |
| S7 | 20000.000000 |
All other variables in the range 1-42 are zero.
4) Problem 22 on page 116 of the textbook.
Let Xijk be the units of product 1 produced on machine i during month j and sold in month k. Let Yijk be the units of product 2 produced on machine i during month j and sold in month k.
A correct formulation is
Maximize 55 (X111 + X211) + 12 (X112 + X212 + X122
+ X222) +
65 (Y111 + Y211) + 32 (Y112 + Y212 + Y122 + Y222)
s.t.
| 4 (X111 + X112) + 7 (Y111 + Y112) <= 500 | (Machine 1 availability in month 1) |
| 3 (X211 + X212) + 4 (Y211 + Y112) <= 500 | (Machine 2 availability in month 1) |
| 4 X122 + 7 Y122 <= 500 | (Machine 1 availability in month 2) |
| 3 X222 + 4 Y222 <= 500 | (Machine 2 availability in month 2) |
| X111 + X211 <= 100 | (Month 1 product 1 sales) |
| Y111 + Y211 <= 140 | (Month 1 product 2 sales) |
| X112 + X212 + X122 <= 190 | (Month 2 product 1 sales) |
| Y112 + Y212 + Y122 <= 130 | (Month 2 product 1 sales) |
All variables non-negative
CPLEX Solution:
Log started (V6.5.3) Sun Oct 1 14:12:51 2000
Problem 'temp.lp' read.
Read time = 0.00 sec.
Maximize
obj: 55 X111 + 55 X211 + 12 X112 + 12 X212 + 12 X122 + 12 X222
+ 65 Y111
+ 65 Y211 + 32 Y112 + 32 Y212 + 32 Y122 + 32 Y222
Subject To
c1: 4 X111 + 4 X112 + 7 Y111 + 7 Y112 <= 500
c2: 3 X211 + 3 X212 + 4 Y211 + 7 Y112 <= 500
c3: 4 X122 + 7 Y122 <= 500
c4: 3 X222 + 4 Y222 <= 500
c5: X111 + X211 <= 100
c6: Y111 + Y211 <= 140
c7: X112 + X212 + X122 <= 190
c8: Y112 + Y212 + Y122 <= 130
Bounds
All variables are >= 0.
Tried aggregator 1 time.
LP Presolve eliminated 3 rows and 5 columns.
Reduced LP has 5 rows, 7 columns, and 13 nonzeros.
Presolve time = 0.00 sec.
Iteration log . . .
Iteration: 1 Objective
= 16285.000000
Primal - Optimal: Objective = 2.4213571429e+04
Solution time = 0.00 sec. Iterations = 5 (0)
Variable Name Solution
Value
X111
100.000000
X122
125.000000
Y111
14.285714
Y211
125.000000
Y212
130.000000
Y222
125.000000
All other variables in the range 1-12 are zero.
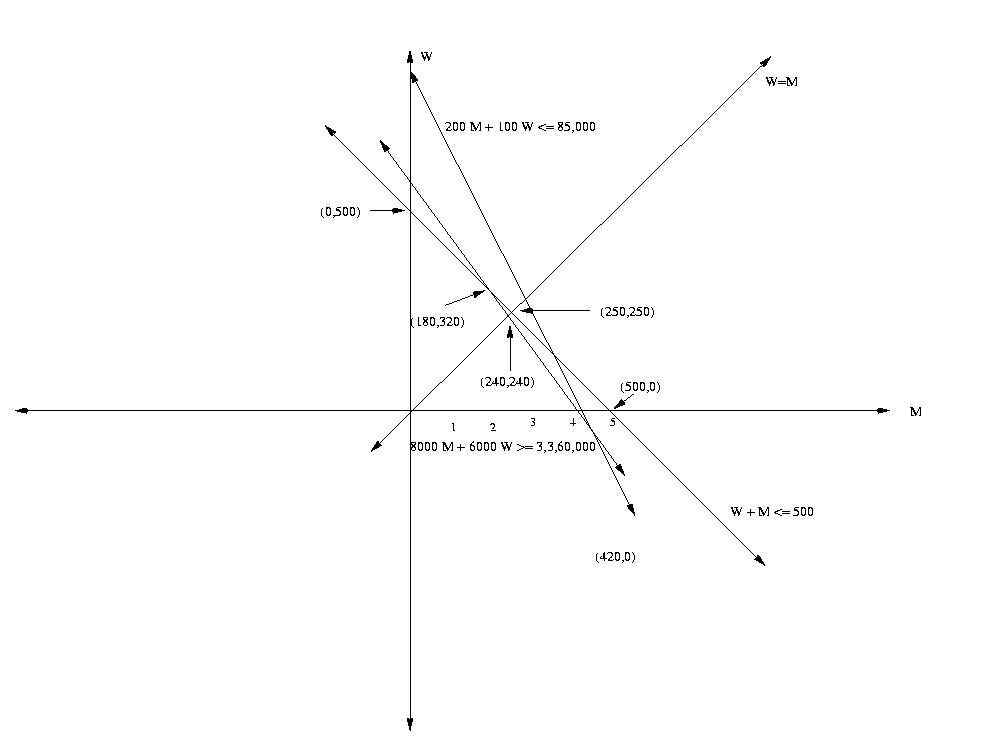
#6) Graphical Solution to the College Admissions Problem
yada yada

| Corner Point | Obj. Value |
| (180,320) | 1,072,000 |
| (240,240) | 1,056,000 |
| (250,250) | 1,100,000 |
The optimal solution is 240 men and 240 women.
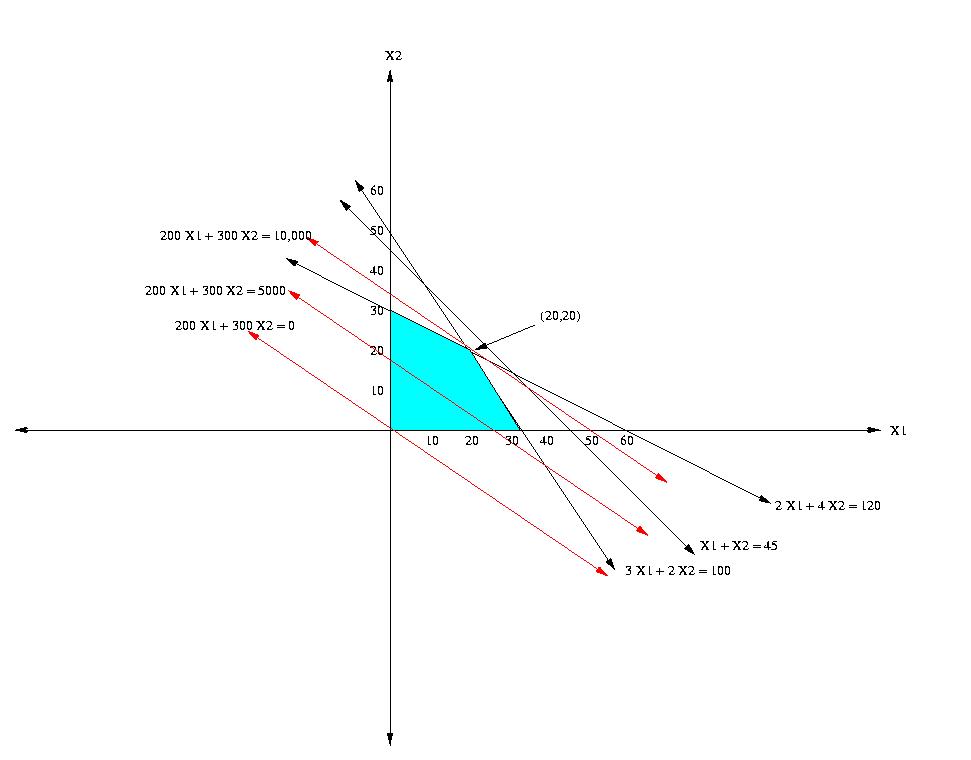
#7) Problem 6 page 64
Let x1 = acres of wheat planted and x2 = acres of corn planted.
A correct formulation is shown below.
max 200 x1 + 300 x2
st
3 x1 + 2 x2 <= 100 Available laborers
2 x1 + 4 x2 <= 120 Available fertiler
x1 + x2 <= 45
Farmer Jane owns 45 acres of land
x1 >= 0
x2 >= 0
Graphical Solution
"Brute Force" Solution
Note that with the non-negativity there a total of 5 contraints giving 10 intersection points.
Constraints 1 and 2:
(3) x1 + (2) x2 = 100
(2) x1 + (4) x2 = 120
x1 = 20.000000, x2 = 20.000000
Feasible. Objective fuction value = 10000.000000.
Constraints 1 and 3:
(3) x1 + (2) x2 = 100
(1) x1 + (1) x2 = 45
x1 = 10.000000, x2 = 35.000000
Infeasible. Constraint 2 is not satisfied.
Constraints 1 and 4:
(3) x1 + (2) x2 = 100
(1) x1 + (0) x2 = 0
x1 = 0.000000, x2 = 50.000000
Infeasible. Constraint 2 is not satisfied.
Constraints 1 and 5:
(3) x1 + (2) x2 = 100
(0) x1 + (1) x2 = 0
x1 = 33.333333, x2 = 0.000000
Feasible. Objective fuction value = 6666.666667.
Constraints 2 and 3:
(2) x1 + (4) x2 = 120
(1) x1 + (1) x2 = 45
x1 = 30.000000, x2 = 15.000000
Infeasible. Constraint 1 is not satisfied.
Constraints 2 and 4:
(2) x1 + (4) x2 = 120
(1) x1 + (0) x2 = 0
x1 = 0.000000, x2 = 30.000000
Feasible. Objective fuction value = 9000.000000.
Constraints 2 and 5:
(2) x1 + (4) x2 = 120
(0) x1 + (1) x2 = 0
x1 = 60.000000, x2 = 0.000000
Infeasible. Constraint 1 is not satisfied.
Constraints 3 and 4:
(1) x1 + (1) x2 = 45
(1) x1 + (0) x2 = 0
x1 = 0.000000, x2 = 45.000000
Infeasible. Constraint 2 is not satisfied.
Constraints 3 and 5:
(1) x1 + (1) x2 = 45
(0) x1 + (1) x2 = 0
x1 = 45.000000, x2 = 0.000000
Infeasible. Constraint 1 is not satisfied.
Constraints 4 and 5:
(1) x1 + (0) x2 = 0
(0) x1 + (1) x2 = 0
x1 = 0.000000, x2 = 0.000000
Feasible. Objective fuction value = 0.000000.
This problem has a unique optimal solution at x1 = 20, x2 = 20.
The objective fuction value = 10000.000000.
LINDO Solution:
MAX 200 X1 + 300 X2
SUBJECT TO
2) 3 X1 + 2 X2 <= 100
3) 2 X1 + 4 X2 <= 120
4) X1 + X2 <= 45
END
LP OPTIMUM FOUND AT STEP 2
OBJECTIVE FUNCTION VALUE
1) 10000.0000
VARIABLE VALUE REDUCED COST
X1 20.000000 .000000
X2 20.000000 .000000
ROW SLACK OR SURPLUS DUAL PRICES
2) .000000 25.000000
3) .000000 62.500003
4) 5.000000 .000000
NO. ITERATIONS= 2
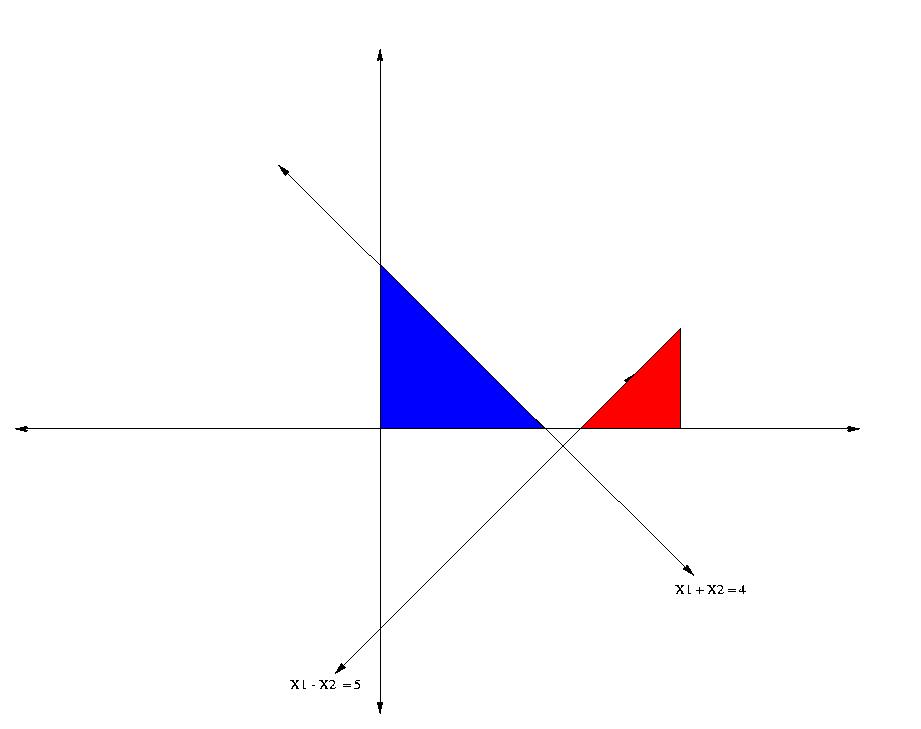
#8) Problem 1 page 69
This problem is infeasible. The blue region in the figure
below indicates
the non-negative points (X1, X2) such that X1 + X2 <= 4. The
red region
in the figure below indicates the non-negative points such that X1
- X2 >= 5.
Since the blue and red regions do not intersect. There are no feasible
points
for this LP.
LINDO Solution:
MAX X1 + X2
SUBJECT TO
2) X1 + X2 <= 4
3) X1 - X2 >= 5
END
NO FEASIBLE SOLUTION AT STEP 1
SUM OF INFEASIBILITIES= 1.00000
VIOLATED ROWS HAVE NEGATIVE SLACK,
OR (EQUALITY ROWS) NONZERO SLACKS.
ROWS CONTRIBUTING TO INFEASIBILITY
HAVE NONZERO DUAL PRICE.
OBJECTIVE FUNCTION VALUE
1) 4.00000000
VARIABLE VALUE REDUCED COST
X1 4.000000 .000000
X2 .000000 2.000000
ROW SLACK OR SURPLUS DUAL PRICES
2) .000000 1.000000
3) -1.000000 -1.000000
NO. ITERATIONS= 1
#9) Problem 2 page 69
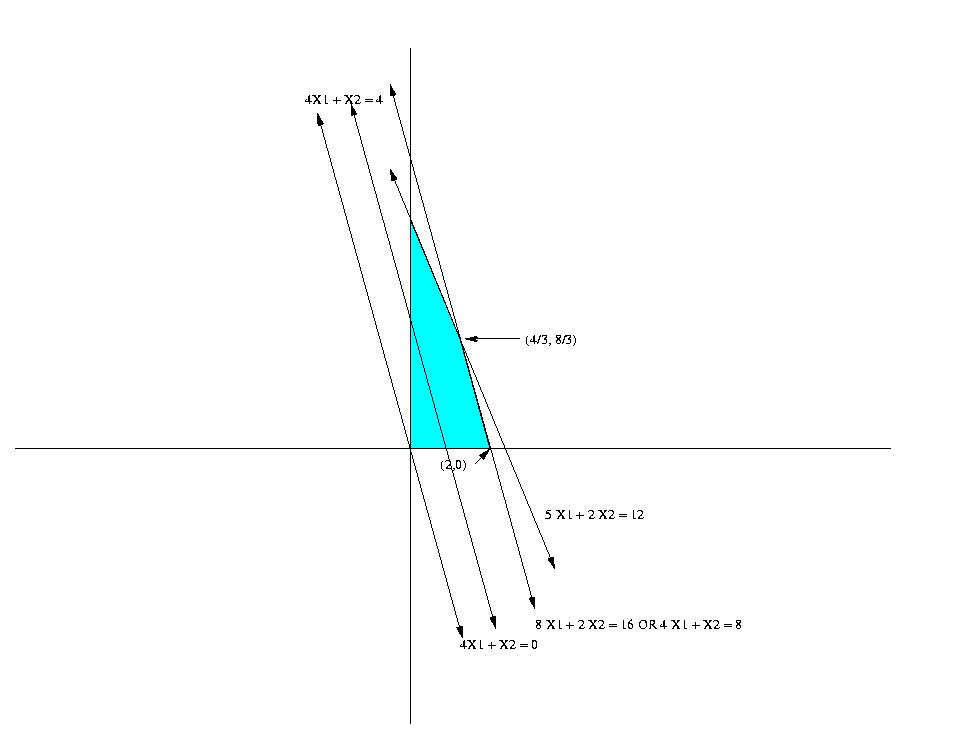
Although LINDO only gives one solution, the problem has multiple optima. Observe that the objective function parallel to the first constraint.
MAX 4 X1 + X2
SUBJECT TO
2) 8 X1 + 2 X2 <= 16
3) 5 X1 + 2 X2 <= 12
END
LP OPTIMUM FOUND AT STEP 1
OBJECTIVE FUNCTION VALUE
1) 8.00000000
VARIABLE VALUE REDUCED COST
X1 .000000 .000000
X2 8.000000 .000000
X2X .000000 .000000
ROW SLACK OR SURPLUS DUAL PRICES
2) .000000 .500000
3) 12.000000 .000000
NO. ITERATIONS= 1
#10) Problem 3 page 70
This problem is unbounded. Any point on the line X1 - X2 = 4 such
that
X1 >=4 is feasible.
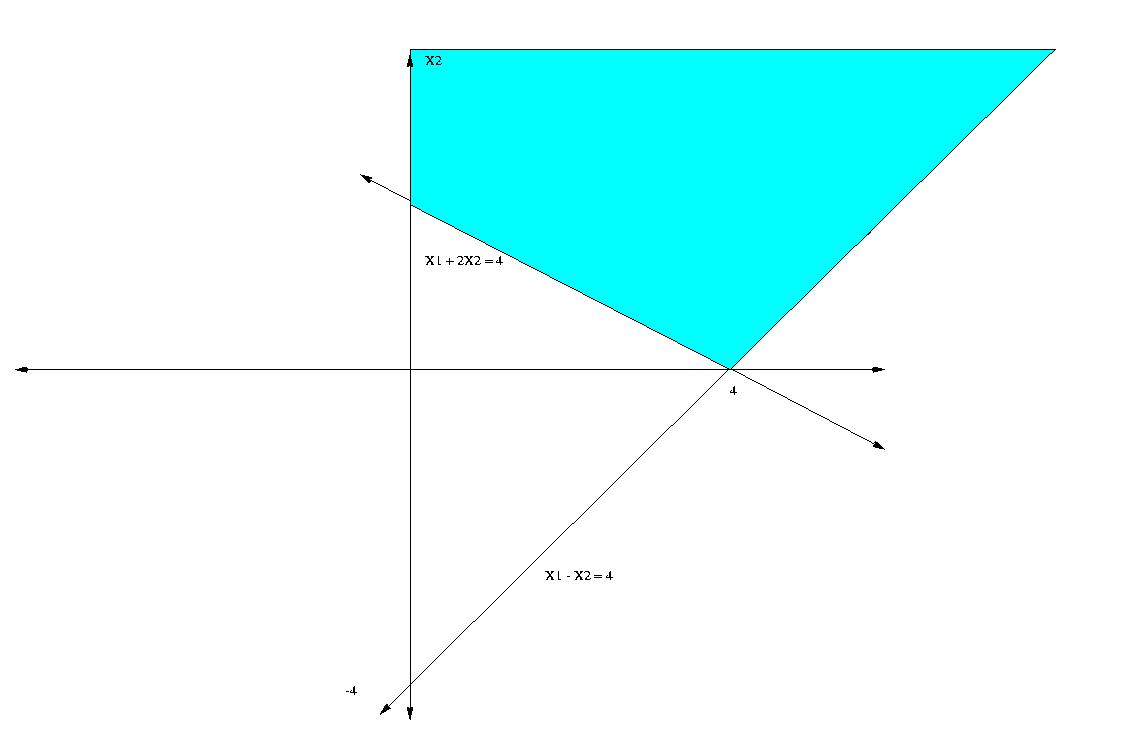
MAX - X1 + 3 X2
SUBJECT TO
2) X1 - X2 <= 4
3) X1 + 2 X2 >= 4
END
UNBOUNDED SOLUTION AT STEP 1
UNBOUNDED VARIABLES ARE:
SLK 3
SLK 2
X2
OBJECTIVE FUNCTION VALUE
1) 6.00000000
VARIABLE VALUE REDUCED COST
X1 .000000 2.500000
X2 99999903.000000 .000000
ROW SLACK OR SURPLUS DUAL PRICES
2) 99999903.000000 .000000
3) .000000 1.500000
NO. ITERATIONS= 1