1) Problem 12 on page 493
Let NY = 1 if the warehouse in New York is opened and 0, otherwise.
Let LA = 1 if the warehouse in LA is opened and 0, otherwise.
Let C = 1 if the warehouse in Chicago is opened and 0, otherwise.
Let A = 1 if the warehouse in Atlanta is opened and 0, otherwise.
The total weekly fixed cost is thus 400 NY + 500 LA + 300 C + 150 A.
The restrictions given in the problem can be modeled as followed:
1) If the New York warehouse is opened, then the LA warehouse must
also be opened.
This means that LA >= NY.
If NY = 1, then LA = 1. However, we can have LA = 1 and NY = 0. This is OK since we can open the LA warehouse without opening the one in New York.
2) Since at most 2 warehouses may be opened, we have NY + LA + C + A <= 2.
3) Either the LA or Atlanta warehouse must be opened, so LA + A >= 1.
Let NY1, NY2 and NY3 be the number of units shipped from the New York warehouse to regions 1, 2 and 3, respectively. LA1, LA2, LA3, C1, C2, C3, A1, A2, and A3 are defined similarly.
Since we cannot ship any items from New York to region 1 if we don't build the warehouse in New York, we have impose the following constraint on our IP:
NY1 <= 100 NY.
If NY = 0, then this forces NY1 to be 0. If NY = 1, then NY1 can take on any value up to o 100 (the maximum number of 2 that may shipped from any warehouse).
In order to satisfy the demand in region 1, we require
NY1 + LA1 + C1 + A1 >= 80.
Finally, we have constraints on the total number of units shipped from
the factories.
For example,
NY1 + NY2 + NY3 <= 100
A complete formulation and solution in CPLEX format are shown below.
Minimize
obj: 400 NY + 500 LA + 300 C + 150 A + 20 NY1 + 40 NY2 + 50 NY3 + 48 LA1
+ 15 LA2 + 26 LA3 + 26 C1 + 35 C2 + 18 C3 + 24 A1 + 50 A2 + 35 A3
Subject To
c1: NY1 + LA1 + C1 + A1 >= 80
c2: NY2 + LA2 + C2 + A2 >= 70
c3: NY3 + LA3 + C3 + A3 >= 40
c4: - NY + LA >= 0
c5: NY + LA + C + A <= 2
c6: LA + A >= 1
c7: - 100 NY + NY1 <= 0
c8: - 100 NY + NY2 <= 0
c9: - 100 NY + NY3 <= 0
c10: - 100 LA + LA1 <= 0
c11: - 100 LA + LA2 <= 0
c12: - 100 LA + LA3 <= 0
c13: - 100 A + A1 <= 0
c14: - 100 A + A2 <= 0
c15: - 100 A + A3 <= 0
c16: - 100 C + C1 <= 0
c17: - 100 C + C2 <= 0
c18: - 100 C + C3 <= 0
c19: NY1 + NY2 + NY3 <= 100
c20: LA1 + LA2 + LA3 <= 100
c21: C1 + C2 + C3 <= 100
c22: A1 + A2 + A3 <= 100
Bounds
0 <= NY <= 1
0 <= LA <= 1
0 <= C <= 1
0 <= A <= 1
NY1 >= 0
NY2 >= 0
NY3 >= 0
LA1 >= 0
LA2 >= 0
LA3 >= 0
C1 >= 0
C2 >= 0
C3 >= 0
A1 >= 0
A2 >= 0
A3 >= 0
Binaries
NY LA C A
Generals
NY1 NY2 NY3 LA1 LA2 LA3 C1 C2 C3 A1 A2 A3
Tried aggregator 1 time.
Reduced MIP has 22 rows, 16 columns, and 56 nonzeros.
Presolve time = 0.00 sec.
Clique table members: 2
Root relaxation solution time = 0.00 sec.
Objective is integral.
Nodes Cuts/
Node Left Objective IInf Best Integer Best Node ItCnt Gap Variable B Parent Depth
0 0 4205.0000 4 4205.0000 8
4605.0000 2 Flowcuts: 3 13
* 2 1 4750.0000 0 4750.0000 4650.0000 18 2.11% A U 1 2
Flow cuts applied: 3
Integer optimal solution: Objective = 4.7500000000e+03
Solution time = 0.02 sec. Iterations = 20 Nodes = 3
Variable Name Solution Value
LA 1.000000
A 1.000000
LA2 70.000000
LA3 30.000000
A1 80.000000
A3 10.000000
All other variables in the range 1-16 are zero.
Build warehouses in Los Angeles and Atlanta.
From LA, send 70 units to Region 2 and 30 to Region 3.
From Atlanta, send 80 units to Region 1 and 10 to Region 3.
2) Problem 14 on page 494 Let xj = 1 if disk j is used and 0, otherwise.
A correct IP formulation and solution are shown below
minimize total_storage: 3*x[1] + 5*x[2] + x[3] + 2*x[4] + x[5] + 4*x[6] + 3*x[7] + x[8] + 2*x[9] + 2*x[10]; s.t. store_file[1]: x[1] + x[2] + x[4] + x[5] + x[8] + x[9] >= 1; s.t. store_file[2]: x[1] + x[3] >= 1; s.t. store_file[3]: x[2] + x[5] + x[7] + x[10] >= 1; s.t. store_file[4]: x[3] + x[6] + x[8] >= 1; s.t. store_file[5]: x[1] + x[2] + x[4] + x[6] + x[7] + x[9] + x[10] >= 1; CPLEX 6.6.0: CPLEX 6.6.0: optimal integer solution; objective 4 5 MIP simplex iterations 0 branch-and-bound nodes x [*] := 1 0 2 0 3 1 4 0 5 1 6 0 7 0 8 0 9 0 10 1 ; For part b, add the following constraint: 2 * x[2] >= x[3] + x[5] If x[3] = 1, or x[5] = 1 (or both), then x[2] is forced to equal 1. The new optimal solution is to use disks 2 and 3.3) Problem 1 on page 514
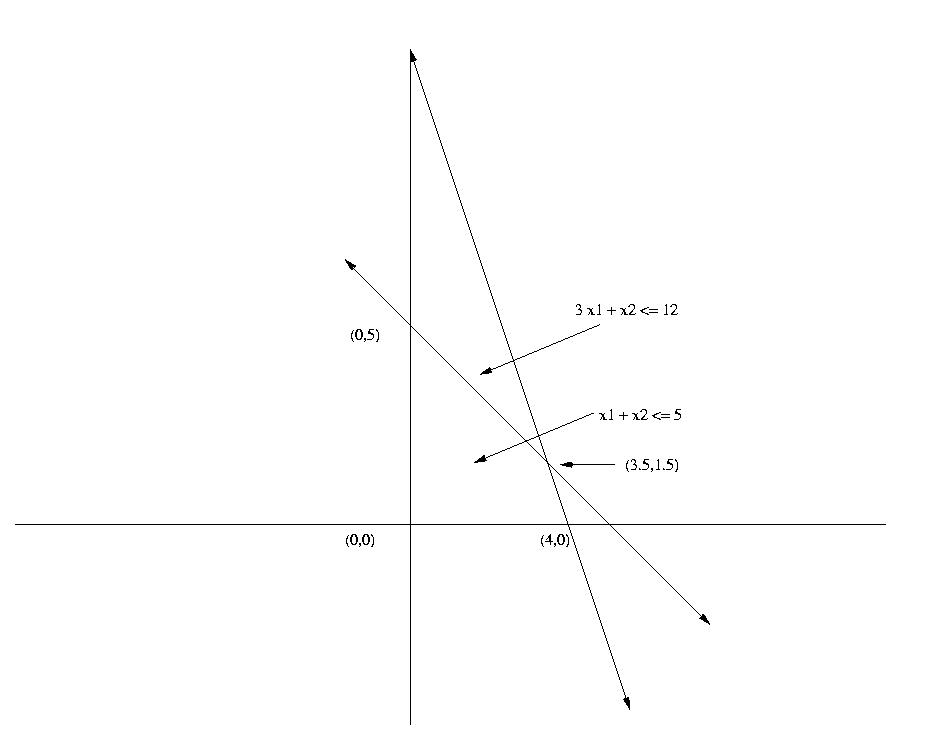
Solving the problem graphically, we see that there are three corner
point solutions
| x1 | x2 | z |
| 0 | 5 | 10 |
| 4 | 0 | 20 |
| 3.5 | 1.5 | 20.5 |

The optimal solution to the LP-relaxation is x1 = 3.5, x2 = 1.5, z= 20.5.
The figure below shows what happens if we branch on x1.
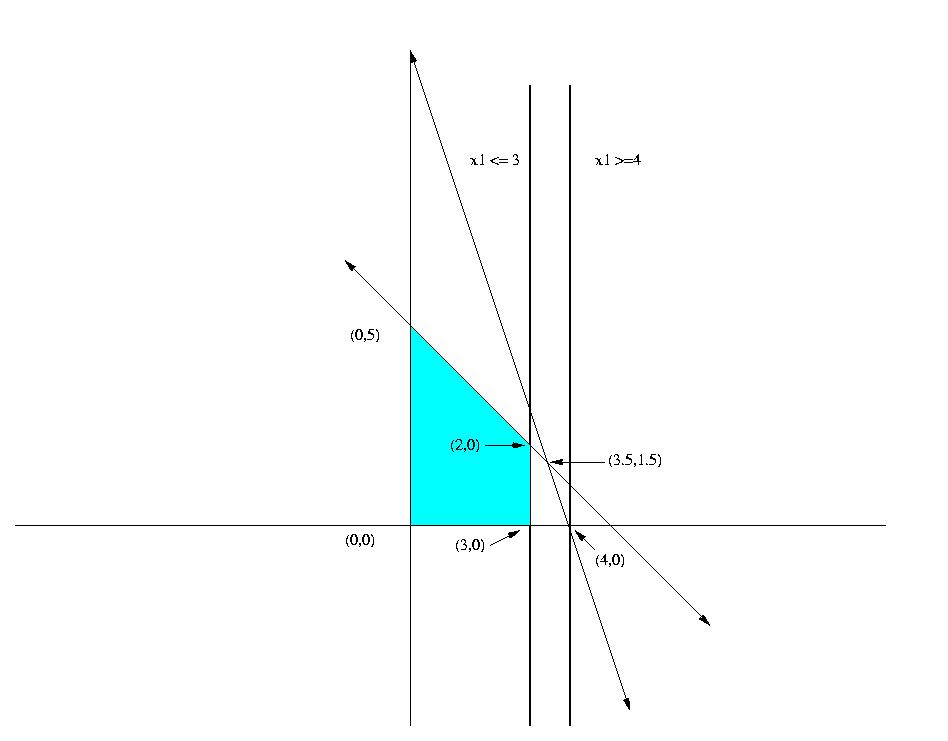
On the ``down'' branch, we add the constraint x1 <= 3. This subproblem
corresponds to the feasible region (shown in blue) to the left of the
line x1 = 3.
To find the optimal solution to this subproblem, we only need to
examine the two new corner point solutions created by adding
this line to the
original feasible region.
Point 1: x1 = 3, x2 = 2, z = 19
Point 2: x1 = 3, x2 = 0, z = 15
Thus, the optimal solution to this subproblem is point 1.
We have an incumbent solution (3,2) with z* = 19.
The other subproblem is created by adding the constraint x3 >= 4 to the original lp-relaxation. This corresponds to adding the line x1 =4 to the original graphical solution and considering solutions in the original feasible region and on , or to the right of, this line. Since x1 = 4, x2 = 0 is the only feasible point in this region, it must be the optimal solution to this subproblem.
Thus, the optimal solution to the original IP is x1 =4, x2 = 0, z = 20.
4) Problem 5 on page 514.
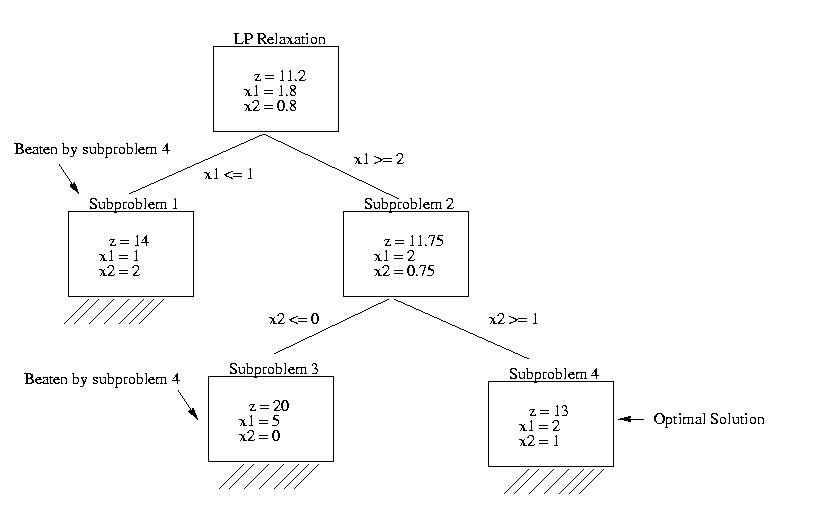
First, we solve the LP relaxation Minimize obj: 4 x1 + 5 x2 Subject To c1: x1 + 4 x2 >= 5 c2: 3 x1 + 2 x2 >= 7 Bounds All variables are >= 0. Primal - Optimal: Objective = 1.1200000000e+01 Variable Name Solution Value x1 1.800000 x2 0.800000 Next, we branch on x1 creating two subproblems. Subproblem 1 (x1 <= 1): Minimize obj: 4 x1 + 5 x2 Subject To c1: x1 + 4 x2 >= 5 c2: 3 x1 + 2 x2 >= 7 c3: x1 <= 1 Bounds All variables are >= 0. Solution: Primal - Optimal: Objective = 1.4000000000e+01 Solution time = 0.00 sec. Iterations = 1 (1) Variable Name Solution Value x1 1.000000 x2 2.000000 Subproblem 2 (x1 >= 2): Minimize obj: 4 x1 + 5 x2 Subject To c1: x1 + 4 x2 >= 5 c2: 3 x1 + 2 x2 >= 7 c3: x1 >= 2 Bounds All variables are >= 0. Primal - Optimal: Objective = 1.1750000000e+01 Solution time = 0.00 sec. Iterations = 1 (1) Variable Name Solution Value x1 2.000000 x2 0.750000 The current branch-and-bound tree is shown below
Since subproblem has integer-valued solution, we can fathom the corresponding node and let x1 = 1, x2 = 2 be the incumbent solution with z*=14. Next, we go to subproblem 2 and branch on x2 creating two new subproblems. Subproblem 3 (x2 <= 0): Since x2 <= 0, the subproblem is Minimize 4 x1 s.t. x1 >= 5 3 x1 >= 7 x1 >= 2 x1 >= 0 Clearly, the optimal solution is x1 = 5, x2 = 0, z = 20. Subproblem 4 (x2 >= 1): Problem addition successful. Minimize obj: 4 x1 + 5 x2 Subject To c1: x1 + 4 x2 >= 5 c2: 3 x1 + 2 x2 >= 7 c3: x1 >= 2 c4: x2 >= 1 Bounds All variables are >= 0. Solution Primal - Optimal: Objective = 1.3000000000e+01 Solution time = 0.00 sec. Iterations = 1 (1) Variable Name Solution Value x1 2.000000 x2 1.000000 The current branch-and-bound tree is shown below.
Since both subproblems 3 and 4 have integer-valued solutions, we can fathom the corresponding nodes of the three. The solution to subproblem 3, (2,1), becomes the new incumbent solution with z*=13. Since all the nodes are fathomed,the branch-and-bound process terminates with the optimal solution x1 = 2, x1 = 1, z = 13.The final branch-and-bound tree is shown below.