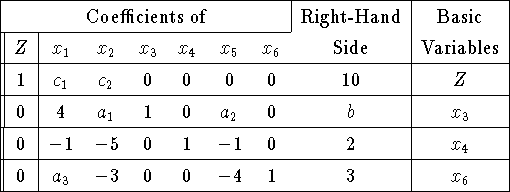
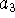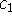State conditions on  ,  ,  , b,  and 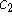 that are required to make the following statements true:

(a) The current solution is not a basic feasible solution.

b < 0. a1, a2, a3, c1 and c3 can be any real numbers.

This gives us a basic solution that is not feasible since it has x3 <0.

(b)The current solution is feasible, but the LP is unbounded.

We need b >= 0 for feasibility.

Given this, the problem is unbounded is c2 < 0 and a1 <= 0.

The other unknowns can be any real numbers.

(c) The current solution is feasible, but the objective function can be improved by replacing 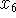 as a basic variable with  .

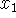We need b >= for feasiblity.

For x1 to enter the basis and improve the solution, we need c1 < 0.

Suppose that x1 enters the basis. The ratio for x3 is b/4, the ratio for x4 is 2/-1 and the ratio for x6 is 3/a3.  Since x4 has a negative ratio, it will not be the exiting variable.

Likewise, we need a3 > 0 for x6 to considered for the exiting variable.

Assuming a3 > 0, x6 will leave the basis if 3/a3 <= b/4.

c2 and a2 can be any real numbers.

(d) The current solution is optimal.

We need b >= 0 for feasibility and c1 >= 0 and c2 >= 0 for the solution to be optimal.

a1, a2 and a3 can be any real numbers.

(e) The current solution is optimal and there is another optimal basic feasible solution.

We need c1 and c2 >= 0 for optimality.
 If b = 0 and a1 > 0, then we can bring x2 into the basis without changing objective function value.

Alternatively, we can b >= 0, c2 = 0 and a1 > 0.
In this case, bringing x2 into the basis will not change the objective function value.

Finally, we can have  b >= 0, c1 = 0 and a3 can be any real number.
In this case, bringing x1 into the basis will not change the objective function value.