basic feasible solution (bfs): a basic solution with all variables >= 0.
In other words, a feasible, basic solution for the
system of linear equations  Ax = b, x >= 0.

pivoting on element a_ij:

1) Divide row i of the augmented matrix A|b by a_ij.
2) For each row k (other than row i), add (- a_kj ) times row i to row k.

The feasible corner-point solutions to an LP are basic feasible solutions. We use pivoting to move from one bfs to a neighboring bfs with an equal or better objective function value.

Pivoting Example:
 

Original LP: Max x + 2 y  st  1) x + y <= 4  2) x - 2 y <= 2  3) -2 x + y <= 2  4) x >= 0  5) y >= 0

Standard Form: Max x + 2 y  st  x + y + s1 = 4  x - 2 y + s2 = 2  -2 x + y + s3= 2  x >= 0 , y >= 0,  s1 >= 0, s2 >= 0, s3 >= 0

The constraints of the Standard Form LP in matrix form

We already have a bfs for the system:

Basic Variables: s1 = 4, s2 = 2, s3 = 2
Non-basic Variables: x = 0, y = 0
(Intersection of constraints 4 and 5 in the original LP)
Objective Function Value = 0.

We can improve the objective function value by increasing the value of x or y.
Pivoting on row 3, column 1 (Increasing x, decreasing s3)

Basic Variables: x = -1, s1 = 5, s2 = 3
Non-Basic Variables: y = 0, s3 = 0
Intersection of constraints 3 and 5.
Corner point, but not feasible.

Pivoting on row 2, column 1 (Increasing x, decreasing s2)

Basic Variables: x=2, s1 =2, s3 =6
Non-Basic Variables: y=0, s2=0
Intersection of constraints 2 and 5.
Feasible.
Objective Function Value = 2.
 
 

Pivoting on row 3, column 2 (Increasing y, decreasing s3)

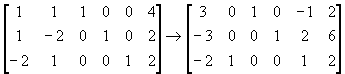
Basic Variables: y = 2, s1 = 4, s2 = 2
Non-Basic Variables: x = 0, s3 = 0
Intersection of constraints 3 and 4. Feasible.
Objective Function Value = 4.

Augmented Matrix form of the LP in Row 0 Form

Basic Variables: z = 0, s1 = 4, s2 = 2, s3 = 2
Non-Basic Variables: x = 0, y =0
Intersection of constraints 4 and 5 (of original LP).
Feasible. Objective Function Value = 0.
 
 

A system of linear equations is in canonical form if each equation has a variable with a coefficient of 1 in that equation and a coefficient of 0 in all other equations.

If an LP is in canonical form, then we can find a basic solution by inspection.

If an LP is in canonical form and all the constraints have nonnegative right-hand sides, then we can find a basic feasible solution by inspection.

If an LP is in row 0 form and the row 1, row 2, ... , row m constraints have nonnegative right-hand sides, then we can find a basic feasible solution and its objective function value by inspection.

Is the current BFS Optimal?

Can we increase the value of z by increasing the value of a non-basic variable?
If we increase x or y, we will have to increase z to maintain the constraint z - x - 2y = 0.
The current solution might not be optimal.

Which non-basic variable should we increase?

A unit increase in x will give us a unit increase in z.
A unit increase in y will give us a two-unit increase in z.
Increase y.

How much can we increase y?

Frome the first constaint:

x + y + s1 = 4 =>

s1 = 4 - y - x

x = 0 =>

s1 = 4 - y

From the second constraint:
x - 2 y + s2 = 2 =>
s2 = 2 - x + 2y

x = 0 =>
s2 = 2 + 2y,

s2 >= 0 =>
2 + 2y >= 0 =>
y >= -1

From the third constraint:
-2 x + y + s3= 2 =>
s3 = 2 + 2x - y

x = 0 =>
s3 = 2 - y

s3 >= 0 =>
2 - y >= 0 =>
y <= 2

We can increase y to 2 if we decrease s3 to 0 at the same time.

Thus, s3 leaves the basis when y enters.
Pivot on Row 3, Column 3

 

Row 0 Form Max z  st  z - x - 2y = 0 x + y + s1 = 4  x - 2 y + s2 = 2  -2 x + y + s3= 2  x >= 0 , y >= 0,  s1 >= 0, s2 >= 0, s3 >= 0	Equivalent Form After Pivot Max z  st  z - 5x + 2 s3 = 4 3x + s1 - s3 = 2  -3x + s2 + 2 s3 = 6 -2 x + y + s3 = 2  x >= 0 , y >= 0,  s1 >=0, s2 >= 0, s3 >=0
Basic Variables:  z, s1, s2 and s3	Basic Variables:  z,y, s1 and s2
Non-Basic Variables: x and y	Non-Basic Variables: x and s3
Obj. Fun. Value: 0	Obj. Fun. Value: 4

Is the current BFS Optimal?

Can we increase the value of z by increasing the value of a non-basic variable?

If we increase x we will have to increase z to maintain the constraint z - 5x + 2 s3 = 4.

The current solution might not be optimal.

Which non-basic variable should we increase?

A unit increase in x will give us a five-unit increase in z.

A unit increase in s3 will give us a two-unit decrease in z.

Increase x.

How much can we increase x?

From the first constraint:

3x + s1 - s3 = 2 =>

s1 = 2 - 3x + s3

s1 >= 0 =>
2 - 3x >= 0 =>
x >= 2/3

From the second constraint:
-3x + s2 + 2 s3 = 6 =>
s2 = 6 + 3x - 2 s3

s3 = 0 =>
s2 = 6 + 3x

s2 >= 0 =>
6 + 3x >= 0 =>
x >= -2
 

From the third constraint:
-2 x + y + s3 = 2 =>
y = 2 + 2x - s3

s3 = 0 =>
y = 2 + 2x,

y >= 0 =>
2 + 2x >= 0 =>
x >= -1

We can increase x to 2/3 if we decrease s1 to 0 at the same time.

Thus, x will enter the basis and s1 will leave.

Pivot on Row 1, Column 2

Is the current BFS Optimal?

Can we increase the value of z by increasing the value of a non-basic variable?

The row 0 constraint is now z + 5/3 s1 + 1/3 s3 = 22/3.

Increasing s1 or s3 could only decrease the value of z.

The solution is optimal.

To see that this is, indeed, an optimal solution, consider the set of equations corresponding to the augmented matrix as shown below.
 
 
 

Row 0 Form Max z  st  z - x - 2y = 0 x + y + s1 = 4  x - 2 y + s2 = 2  -2 x + y + s3= 2  x >= 0 , y >= 0,  s1 >= 0, s2 >= 0, s3 >= 0	Equivalent Form After Second Pivot Max z  st  z + 5/3 s1 + 1/3 s3 = 22/3 x + /13 s1 - 1/3 s3 = 2/3 s1 + s2 + s3 = 8 y + 2/3 s1 + 1/3 s3 = 10/3  x >= 0 , y >= 0,  s1 >= 0, s2 >= 0, s3 >= 0
Basic Variables:  z, s1, s2 and s3	Basic Variables:  z, x, y and s2
Non-Basic Variables: x and y	Non-Basic Variables: s1 and s3
Obj. Fun. Value: 0	Obj. Fun. Value: 22/3

Since we want to make z as large as possible, we want to make s1 and s3 as small as possible. Since s1 and s3 must be >= 0, z = 22/3 is the maximum possible value for the objective function.