Using AMPL

• AMPL a modeling language for mathematical programming (hence the name). While AMPL does not actually solve mathematical programs by itself, it is an extremely useful language for formulating problems which can then be solved by CPLEX or another solver.
•  AMPL is available on all of the SEAS machines named after Simpsons characters: Homer, Marge, Bart, Lisa and Maggie.
•  The AMPL book by Fourer, Gay and Kernighan comes with a CD-rom that has a student version of AMPL and CPLEX for Windows and Windows NT. You can also download the student versions of AMPL and CPLEX from www.ampl.com.

The GT Railroad Problem in AMPL

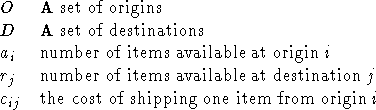
Recall the GT Railroad problem from the Mathematical Programming Examples. Here is one way in which the problem can be formulated and solved via AMPL. Notice that the format is similar to CPLEX's.

ampl: var x11 >= 0;
ampl: var x12 >= 0;
ampl: var x13 >= 0;
ampl: var x14 >= 0;
ampl: var x21 >= 0;
ampl: var x22 >= 0;
ampl: var x23 >= 0;
ampl: var x24 >= 0;
ampl: var x31 >= 0;
ampl: var x32 >= 0;
ampl: var x33 >= 0;
ampl: var x34 >= 0;

ampl: minimize cost: 13 * x11 + 35 * x12 + 42 * x13 + 9 * x14 + 
6 * x21 + 61 * x22 + 18 * x23 + 30 * x24 + 
15 * x31 + 10 * x32 + 5 * x33 + 9 *x34;


ampl: subject to IE_Junction: x11 + x12 + x13 + x14 <= 4; 
ampl: subject to Centerville: x21 + x22 + x23 + x24 <= 1;
ampl: subject to Wayover_City: x31 + x32 + x33 + x34 <= 2; 
ampl: subject to A_Station: x11 + x21 + x31 >= 1; 
ampl: subject to Fine_Place: x12 + x22 + x32 >= 1; 
ampl: subject to Goodville: x13 + x23 + x33 >= 1; 
ampl: subject to Somewhere_Street: x14 + x24 + x34 >= 1; 

ampl: solve;
CPLEX 6.6.0: 
CPLEX 6.6.0: optimal solution; objective 30
8 simplex iterations (4 in phase I)


ampl: display x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34;
x11 = 0
x12 = 0
x13 = 0
x14 = 1
x21 = 1
x22 = 0
x23 = 0
x24 = 0
x31 = 0
x32 = 1
x33 = 1
x34 = 0

A More General Model
This problem can be viewed as specific instance of a more
general problem. Given,

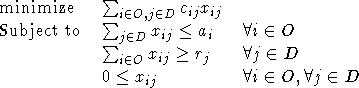
The General Model in AMPL

A convenient feature of AMPL is that it allows you to store the mathematical formulation and a data for a problem separately. For example, we can store the formulation for the more general model above in an AMPL file called transport_model.txt which would look like this:

set O;
set D;
param a {i in O};
param r {j in D};
param c {i in O, j in D};
var x {i in O, j in D} >= 0;
minimize cost: sum {i in O, j in D} c[i,j] * x[i,j];
subject to supply {i in O}: sum {j in D} x[i,j] <= a[i];
subject to demand {j in D}: sum {i in O} x[i,j] >= r[j];

To solve the problem for a specific instance, say the original example in this handout, we can create a file called GT_data.txt which would look like this.

set O := IE_Junction, Centerville, Wayover_City;
set D := A_Station, Fine_Place, Goodville, Somewhere_Street;

# supply
param a :=
IE_Junction     4
Centerville     1
Wayover_City    2;

# demand
param r :=
A_Station       1
Fine_Place      1
Goodville       1
Somewhere_Street        1;


param c :
                A_Station       Fine_Place      Goodville       Somewhere_Street :=
IE_Junction     13              35              42              9
Centerville     6               61              18              30
Wayover_City    15              10              5               9;

Here is how we would then solve the problem in AMPL.

ampl: model trans_model.txt;
ampl: data  GT_data.txt;
ampl: solve;

CPLEX 6.6.0: 
CPLEX 6.6.0: optimal solution; objective 30
8 simplex iterations (4 in phase I)

ampl: display x;

x :=
Centerville  A_Station          1
Centerville  Fine_Place         0
Centerville  Goodville          0
Centerville  Somewhere_Street   0
IE_Junction  A_Station          0
IE_Junction  Fine_Place         0
IE_Junction  Goodville          0
IE_Junction  Somewhere_Street   1
Wayover_City A_Station          0
Wayover_City Fine_Place         1
Wayover_City Goodville          1
Wayover_City Somewhere_Street   0
;

To see how AMPL combines the model and data files into an LP, we can use the "expand" command:

ampl: expand;

minimize cost:
        13*x['IE_Junction','A_Station'] + 35*x['IE_Junction','Fine_Place'] + 
        42*x['IE_Junction','Goodville'] + 9*x['IE_Junction','Somewhere_Street']
         + 6*x['Centerville','A_Station'] + 61*x['Centerville','Fine_Place'] + 
        18*x['Centerville','Goodville'] + 
        30*x['Centerville','Somewhere_Street'] + 
        15*x['Wayover_City','A_Station'] + 10*x['Wayover_City','Fine_Place'] + 
        5*x['Wayover_City','Goodville'] + 
        9*x['Wayover_City','Somewhere_Street'];

s.t. supply['IE_Junction']:
        x['IE_Junction','A_Station'] + x['IE_Junction','Fine_Place'] + 
        x['IE_Junction','Goodville'] + x['IE_Junction','Somewhere_Street'] <= 4;

s.t. supply['Centerville']:
        x['Centerville','A_Station'] + x['Centerville','Fine_Place'] + 
        x['Centerville','Goodville'] + x['Centerville','Somewhere_Street'] <= 1;

s.t. supply['Wayover_City']:
        x['Wayover_City','A_Station'] + x['Wayover_City','Fine_Place'] + 
        x['Wayover_City','Goodville'] + x['Wayover_City','Somewhere_Street']
         <= 2;

s.t. demand['A_Station']:
        x['IE_Junction','A_Station'] + x['Centerville','A_Station'] + 
        x['Wayover_City','A_Station'] >= 1;

s.t. demand['Fine_Place']:
        x['IE_Junction','Fine_Place'] + x['Centerville','Fine_Place'] + 
        x['Wayover_City','Fine_Place'] >= 1;

s.t. demand['Goodville']:
        x['IE_Junction','Goodville'] + x['Centerville','Goodville'] + 
        x['Wayover_City','Goodville'] >= 1;

s.t. demand['Somewhere_Street']:
        x['IE_Junction','Somewhere_Street'] + 
        x['Centerville','Somewhere_Street'] + 
        x['Wayover_City','Somewhere_Street'] >= 1;

Now, suppose the three locomotives are available at each origin and that two are required at each destination. We can edit the file GT_data.txt as shown below and solve the problem again.

set O := IE_Junction, Centerville, Wayover_City;
set D := A_Station, Fine_Place, Goodville, Somewhere_Street;

# supply
param a :=
IE_Junction     3
Centerville     3
Wayover_City    3;

# demand
param r :=
A_Station       2
Fine_Place      2
Goodville       2
Somewhere_Street        2;


param c :
                A_Station       Fine_Place      Goodville       Somewhere_Street :=
IE_Junction     13              35              42              9
Centerville     6               61              18              30
Wayover_City    15              10              5               9;

Here are the results:

ampl: model trans_model.txt;
ampl: data GT_data.txt;
ampl: solve;


CPLEX 6.6.0: 
CPLEX 6.6.0: optimal solution; objective 73
11 simplex iterations (6 in phase I)

ampl: display x;

x :=
Centerville  A_Station          2
Centerville  Fine_Place         0
Centerville  Goodville          1
Centerville  Somewhere_Street   0
IE_Junction  A_Station          0
IE_Junction  Fine_Place         0
IE_Junction  Goodville          0
IE_Junction  Somewhere_Street   2
Wayover_City A_Station          0
Wayover_City Fine_Place         2
Wayover_City Goodville          1
Wayover_City Somewhere_Street   0
;

Odds and Ends

• To end an AMPL session, type "quit;" at the ampl prompt.
•  You can't print directly from AMPL. Instead, you need to save your output to a file. To write output to a file called "results", use the command


ampl: display x > results;

This will write the values of the x variables to the file "results".

•  Sometimes you may mistakes in your model or data. And so, you read in the file, discover the error, edit the file and then try to read it in again. If you do this, AMPL will complain. There are a couple of ways to get around this. One way is to just quit and restart AMPL. Another way is to type the command reset before reading in the model the second time.

 

 

• About this document ...

Thu Oct 19 17:46:20 CDT 2000