
Balloon-powered Car
Why is this important?
We learned from the discussion of jet engines that they generate thrust by accelerating fluid away from them at a high rate of speed. Turbojets do this using a complex combination of machinery and combustion, but we can emulate the basic mechanism using a balloon, which accelerates stored air away from it as it deflates. A balloon, however, does not work exactly the same as a jet engine because it pushes stored air while a jet engine brings air in and pushes it out at the same time. Nevertheless, we can investigate some of the key characteristics of jet propulsion using a balloon-powered car.
[Note: Although jets and propellers have key differences, much of the basic physics is the same, so many of the procedures in this activity will be similar to those in Activity 1 (Propeller-driven car).]
What do I need?
A balloon powered car [recommended balloon-powered car kit: Doc Fizzix Balloon-powered Racer. Material required to assemble the kit: wood glue, a ruler, a pencil, and needle-nosed pliers.]
Measuring tape
Piece of paper
Stopwatch
Scale or balance
Procedure
Assemble the car according to the instructions included with the kit. Be careful to follow the instructions carefully. When you are finished it should look something like the picture shown below.

Find the mass of the vehicle using the scale or balance. The car will have two configurations with two different nozzle sizes. A 10 mm diameter nozzle/tube (included with the kit) and a 5-6mm diameter tube (which you will need to purchase separately). Make sure to weigh the car with both nozzles. When you are finished assembling and weighing the car you are ready to make some measurements of propulsive performance.
Range
When you blow up the balloon, you are storing energy in the balloon that is released when you let the car go. The more air you blow into the balloon, the more energy you sore and therefore, the further the car should go. Equivalently, the larger the diameter of the balloon after you fill it with air (D), the further the car should go. To investigate this we will measure the range of the propeller car with both the large and small nozzle for different initial balloon diameters.
Procedure:

| D = 15 cm | D = 20 cm | D = 25 cm | |
|---|---|---|---|
| Large nozzle | |||
| Small nozzle |
When you have completed the table, make a plot of R vs. D. Include the results for both nozzle diameters on the plot so you can compare them. D is the independent variable in this experiment, so put it on the horizontal axis.
Thrust
In the range experiments, you probably observed that the car accelerates while the balloon deflates and then it coasts to a stop after the air has left the balloon. By Newton's 2nd Law, the car accelerates in proportion to the thrust applied by the jet as the balloon deflates. Thus, we can measure the average thrust supplied by the jet by measuring the car acceleration.
Procedure:
| D = 15 cm | D = 20 cm | D = 25 cm | |
|---|---|---|---|
| Large nozzle | L: t: |
L: t: |
L: t: |
| Small nozzle | L: t |
L: t: |
L: t: |
Assuming approximately constant acceleration while the balloon deflates, acceleration may be computed from
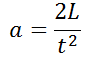
Then thrust may be computed from Newton's 2nd Law, namely,
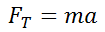
where m is the mass of the car measured earlier. Compute thrust for each of the measurements made. Make a plot of FT vs. D for both nozzle sizes.
Efficiency
As discussed in the Principles section, overall efficiency is the ratio of power output to rate of energy input. Or equivalently, it is the work output over the total energy input. In this case, the jet is doing work only while the balloon is deflating (no work is done by the jet during the coasting phase). Thus the work done by the propulsion system is
The energy used for propulsion is stored while the balloon is being inflated. This energy is approximately proportional to D2 - D20, where D0 is the initial diameter of the balloon (measured by laying the balloon flat before filling it with air). Thus we may say the efficiency obeys
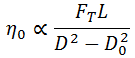
Compute  for the data taken in the thrust experiment and plot
for the data taken in the thrust experiment and plot  vs. D. Note that we are not computing efficiency directly, only something that is proportional to efficiency. Also, we have assumed thrust is constant during car acceleration (which is not precisely true). Nevertheless, your plot of
vs. D. Note that we are not computing efficiency directly, only something that is proportional to efficiency. Also, we have assumed thrust is constant during car acceleration (which is not precisely true). Nevertheless, your plot of  vs. D should give an approximate indication of how efficiency depends on D and nozzle size.
vs. D should give an approximate indication of how efficiency depends on D and nozzle size.
What did you observe?
Range
How does range depend on D? Does it follow the expected trend? Based on your measurements, what could you do to improve range?
Thrust
The general equation for thrust is
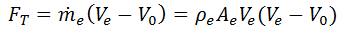
For the balloon car, there is no inlet, so V0 = 0 and the equation reduces to
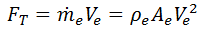
where Ae is the area of the nozzle and Ve is the velocity of the jet. Using this equation, what do your results indicate about how changing Ae affects thrust? Is Ae the only thing in the thrust equation that is changed when the nozzle diameter is changed? If not, how can you tell?
How does changing D affect thrust? Why? Hint: Think about changing pressure in the balloon will affect Ve and how changing D affects the pressure in the balloon.
Efficiency
How does changing D affect efficiency? Which nozzle size was more efficient? For the balloon car, the thermal efficiency of the balloon is close to 1, so the overall efficiency and propulsive efficiency are approximately the same (η0 ≈ ηp). Because the balloon does not intake air as it propels the car, the equation for propulsive efficiency is modified to
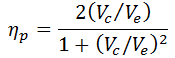
where Vc is the speed of the car. Use this equation to explain your observations about propulsive efficiency. Hint: think about how changing D or jet diameter affects Ve.
