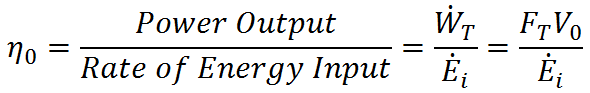
Efficiency
The 1st Law of Thermodynamics indicates that the “cost” or “input” required to generate propulsion (do work with a propulsion system) is energy. For mechanical propulsion, this energy comes from chemical energy in fuel or nuclear energy (in the case of nuclear submarines). For animals, the energy comes from the food they eat. In either case, it is desirable to do a lot of work with very little energy input (get more “bang for your buck,” so to speak). To quantify the relationship between work output and energy input we define overall efficiency as
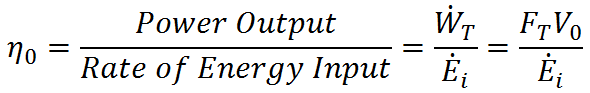
where 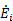 is the rate of energy input required to generate the given thrust. High η0 indicates low energy input for a given work output. The 1st Law of Thermodynamics, however, indicates that the maximum overall efficiency is η0 = 1, which occurs when there is no heat transfer out of the system (all incoming energy is converted to work). In reality, η0 < 1 due to limitations of the 2nd Law of Thermodynamics.
is the rate of energy input required to generate the given thrust. High η0 indicates low energy input for a given work output. The 1st Law of Thermodynamics, however, indicates that the maximum overall efficiency is η0 = 1, which occurs when there is no heat transfer out of the system (all incoming energy is converted to work). In reality, η0 < 1 due to limitations of the 2nd Law of Thermodynamics.
For mechanical propulsion systems like jet engines and propeller-based propulsion, η0 is traditionally split into two parts: thermal efficiency and propulsive efficiency.
Propulsive efficiency (ηp) measures the effectiveness of a propulsive device in converting mechanical power input (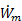 ) to propulsive power output (thrust power,
) to propulsive power output (thrust power, 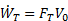 ). Taking the ratio of output to input, propulsive efficiency is defined as
). Taking the ratio of output to input, propulsive efficiency is defined as
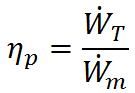
In the case of a propeller, 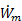 is the power required from the motor to spin the propeller.
is the power required from the motor to spin the propeller.
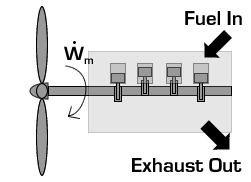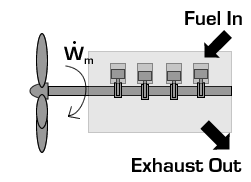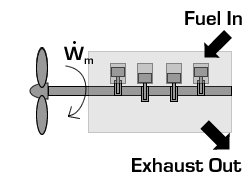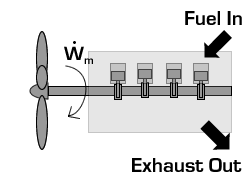
Due to conservation of energy in the conversion process, 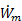 is identical to the kinetic energy added to the fluid by the propulsion device. Using the kinetic energy equivalence of
is identical to the kinetic energy added to the fluid by the propulsion device. Using the kinetic energy equivalence of 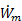 together with
together with 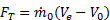 for steady-state propulsion, the general definition for propulsive efficiency can be simplified to
for steady-state propulsion, the general definition for propulsive efficiency can be simplified to
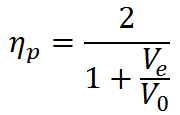
Since Ve > V0 to generate thrust, we see that ηp < 1 according to this formula. The physical reason for ηp < 1 is that not all of the mechanical power 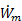 goes into propelling the vehicle; some of it is left behind as extra or "excess" kinetic energy in the fluid (the fluid is not motionless after the vehicle passes by). This effect can be minimized by using a Ve very close to the vehicle velocity V0 and ηp approaches one as Ve approaches V0. Thus, high propulsive efficiency is achieved by accelerating fluid only a small amount. In this limit, thrust is very small unless
goes into propelling the vehicle; some of it is left behind as extra or "excess" kinetic energy in the fluid (the fluid is not motionless after the vehicle passes by). This effect can be minimized by using a Ve very close to the vehicle velocity V0 and ηp approaches one as Ve approaches V0. Thus, high propulsive efficiency is achieved by accelerating fluid only a small amount. In this limit, thrust is very small unless 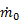 is very large (remember,
is very large (remember, 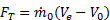 ). A large
). A large 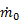 means that the amount of fluid mass moving through the propulsion system is large, which requires a large propulsion device. To achieve high propulsive efficiency with acceptable thrust levels requires a compromise between size and efficiency!
means that the amount of fluid mass moving through the propulsion system is large, which requires a large propulsion device. To achieve high propulsive efficiency with acceptable thrust levels requires a compromise between size and efficiency!
Thermal efficiency (ηth) is the effectiveness of a propulsion system in converting the input energy (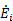 ) to mechanical power (
) to mechanical power (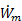 ). That is,
). That is,
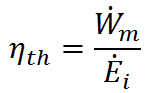
The reason we call this ratio thermal efficiency is that most mechanical power systems use a high temperature source of thermal energy to do work. These systems are called heat engines, and examples include the internal combustion engine in your car (which uses hot gases from the combustion of fuel and air to turn the motor) and nuclear reactors (which use nuclear fuel to boil water and the resulting steam turns a motor). In order for heat engines to do work, they must expell any unused energy to a low temperature heat sink. For example, internal combustion engines exhaust the hot gases to the cool atmosphere. The magnitude of thermal efficiency for heat engines is governed by the conversion of energy input from the high temperature energy source into mechanical output. Due to the 2nd Law of Thermodynamics, ηth < 1, but ηth increases as the temperature difference between the high temperature energy souce (TH) and low temperature sink (TL) increases.
Thermal efficiency of heat engines is limited by the Carnot efficiency. Carnot efficiency describes the thermal efficiency of an idealized heat engine that utilizes the energy of the high temperature energy source to the maximum possible extent and eliminates potential energy losses such as friction from the system. The Carnot efficiency is given by
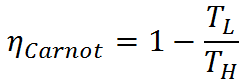
Because the Carnot efficiency is based on an idealized engine without friction or other drawbacks, it is not achievable in real world applications. The Carnot efficiency is nevertheless useful in delimiting the maximum possible efficiency of real heat engines, and it may be approached with careful engine design.
From the definitions of propulsive and thermal efficiency, it is clear that
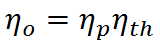
If overall efficiency governs the overall performance of a propulsion system, the distinction between thermal and propulsive efficiency may seem unnecessary. The distinction is most useful for propeller-based propulsion systems where ηth is governed by the design of the engine spinning the propeller and ηp is governed by the propeller design. That is, knowing ηth and ηp allows one to evaluate if both components of the system are achieving peak performance and if not, where attention should be focused to obtain the greatest gains.
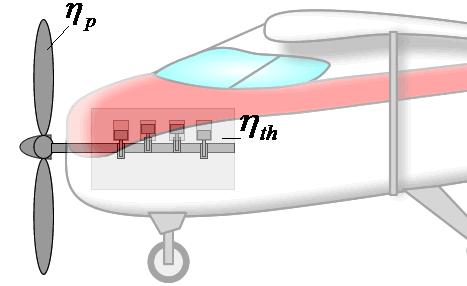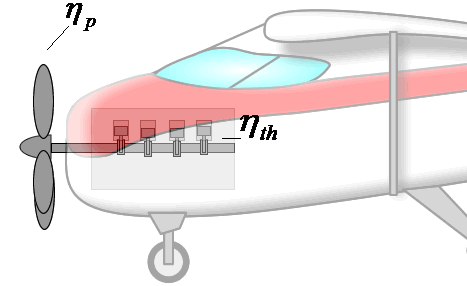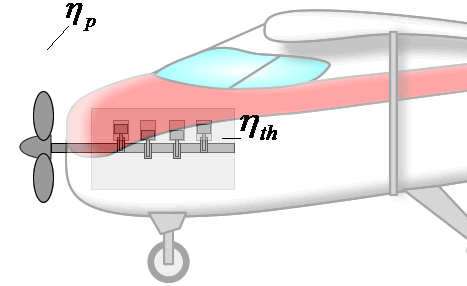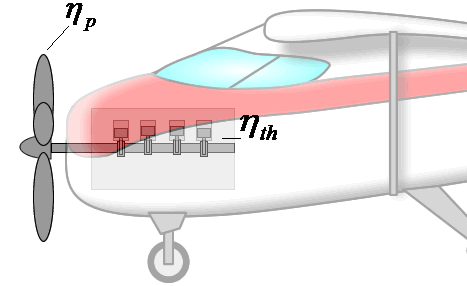
Components are more integrated in jet engines than propeller propulsion systems, but distinguishing the contributions of propulsive and thermal efficiency is still useful for jet engines. These issues will be discussed in more detail in the Design section.
For biological systems, “thermal” efficiency is determined by the efficiency of the animal muscles in converting chemical energy into mechanical power and propulsive efficiency has the same meaning as described above. These two components of overall efficiency can be difficult to determine for biological propulsion because food intake is used for more than just propulsion (making ηth difficult to determine) and the propulsion system is typically unsteady and integrated into the animal body (making 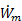 difficult to measure or compute). Nevertheless, when they can be determined these quantities are useful for comparing the performance and behavior of different animal species on equal footing. They are also useful for comparing biological propulsion systems with equivalent mechanical systems such as micro-air vehicles (MAVs) or mini submarines.
difficult to measure or compute). Nevertheless, when they can be determined these quantities are useful for comparing the performance and behavior of different animal species on equal footing. They are also useful for comparing biological propulsion systems with equivalent mechanical systems such as micro-air vehicles (MAVs) or mini submarines.

|
Example Problem: Efficiency Analysis |
