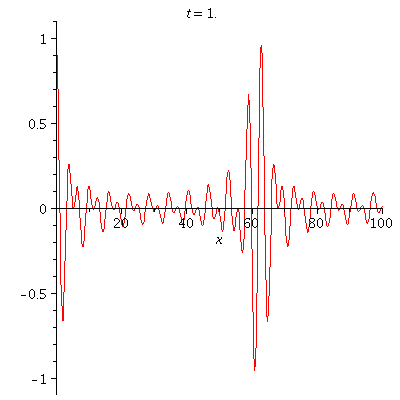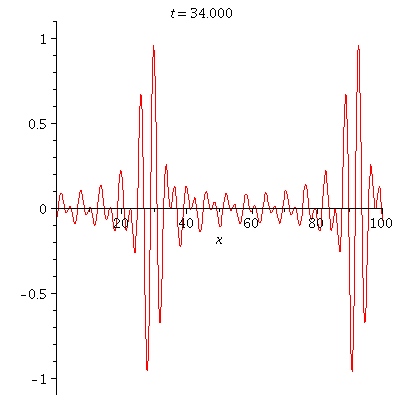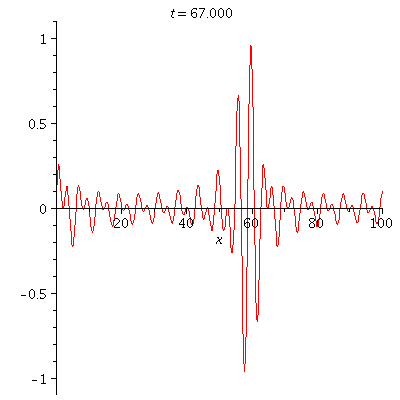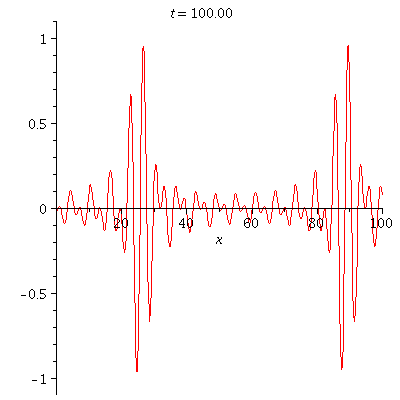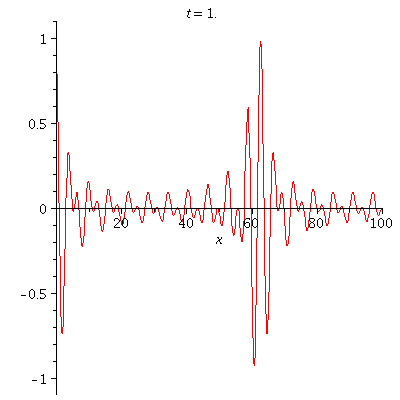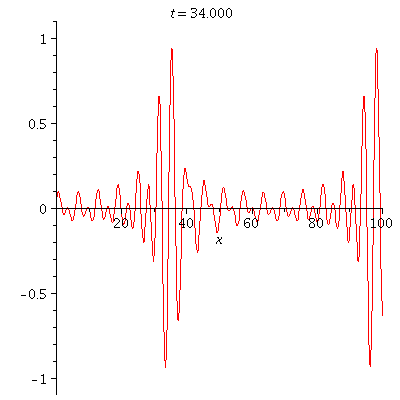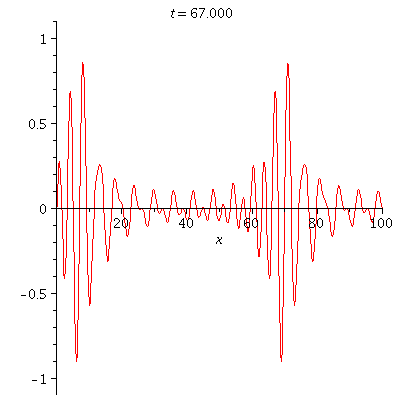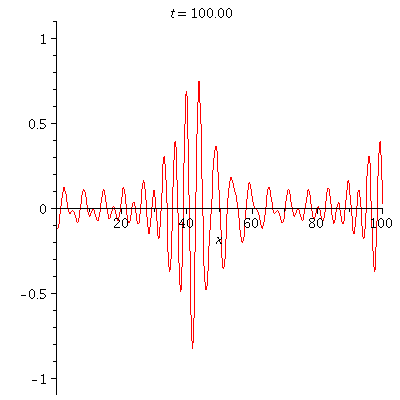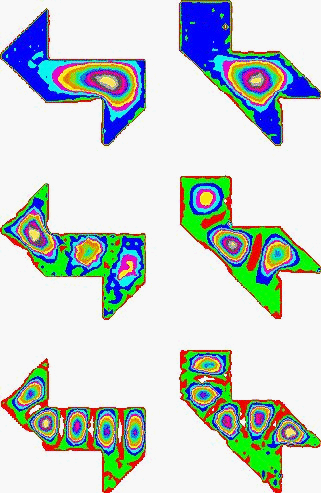
| = | |||
| = |
(The figures to the right are from Dr. Srinivas Sridhar at http://sagar.physics.neu.edu/isospec.html )
The method presented adds a function b(x,y) so that the the boundary condition at the corners of the new function v is always 0. Notice that b is "bi"-linear so that the Laplacian(b) = 0.
While there are some new terms the paper is not too difficult to read. Note that the solution method where u is solved for in four different parts appears in section 2.5 of our book.
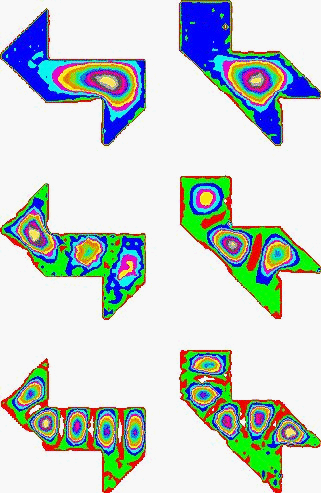 |
Mark Kac's question is a translation of the question, knowing the
spectrum, i.e., the eigenvalues, of the Laplacian with Dirichlet
boundary conditions, can we determine the shape of the
boundary?
(The figures to the right are from Dr. Srinivas Sridhar at http://sagar.physics.neu.edu/isospec.html ) |
In the figures above Dr. Sridhar shows the first three eigenfunctions for two different microwave cavities. They experimentally confirmed an earlier theoretical result by Gordon, Webb and Wolpert (1992) that the eigenvalues for each cavity (drum) were the same.
An easy "popular press" article on this subject appear in Science News. Dr. Sridhar's web page has more information on the microwave cavity experiments. Dr. Tony Driscal has recently improved techniques to compute the eigenvalues of isospectral drums.
| Search online for photots and videos os "Jaws waves". Here is some cool physics . |
 |