Exercise 2-10

An important problem for airlines is the determination of how much fuel an airplane should load at each stop. Since the efficiency of an airplane is related to its weight, an airplane fully loaded with fuel burns more fuel per mile in flight. This fact argues for planes filling up at each stop with just enough fuel to take them to their next stop.

Unfortunately, since fuel prices vary substantially from one location to another, this policy of minimal fill-ups may be more costly than filling the tank at an inexpensive location. Airlines need to achieve the appropriate balance since fuel costs are, by far, the single largest item in airlines' costs.

Consider the small example of an airplane that flies the following ``rotation:" Los Angeles Tampa Miami Ft. Lauderdale New York Ft. Lauderdale Miami Houston Los Angeles (completing a cycle). Table 1 shows, for each leg and city i, , the fuel cost per gallon in city i; , the minimum gallons of fuel needed to get from i to the next stop; and , the additional fuel (in 0.01 gallons) burned per gallon of fuel loaded over the minimum, .

 
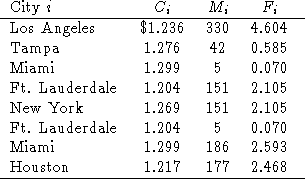
Table 1: Fuel Costs and Requirements  

For example, in Los Angeles, the airplane could be loaded with 330 gallons, which would just make it to Tampa. Alternatively, in order to fill up with enough fuel in LA to get to Miami without refueling at Tampa, gallons would be required. The last term represents the extra fuel burned on the trip from Los Angeles to Tampa due to the presence of the additional 42 gallons loaded in LA.

Comparing costs for these two simple alternatives:

• Alternative 1. Minimum fill-up in LA ( ) plus the minimum fill-up in Tampa ( ) = $461.47
• Alternative 2. 373.934-gallon fill-up in LA

shows the former to be less costly. The cost of additional fuel (almost two gallons) needed for the larger fill-up in LA is greater than the cost savings due to the less-expensive fuel in LA.

Formulate a linear program to determine the least-cost locations and fill-up amounts for the rotation above.