Overview
My research concerns:
(1) developing and transforming fast algorithms in scientific computing to resolve fundamental computational issues in statistics, machine learning and deep learning;
(2) incorporating machine learning techniques into scientific computing to break bottlenecks such as complex data distribution, curse of dimensionality;
(3) resolving high dimensional data algorithmically and theoretically.
Research Interests
- Hierarchical Data Compression, Deep Learning, Manifold Learning, Bayesian Optimization...
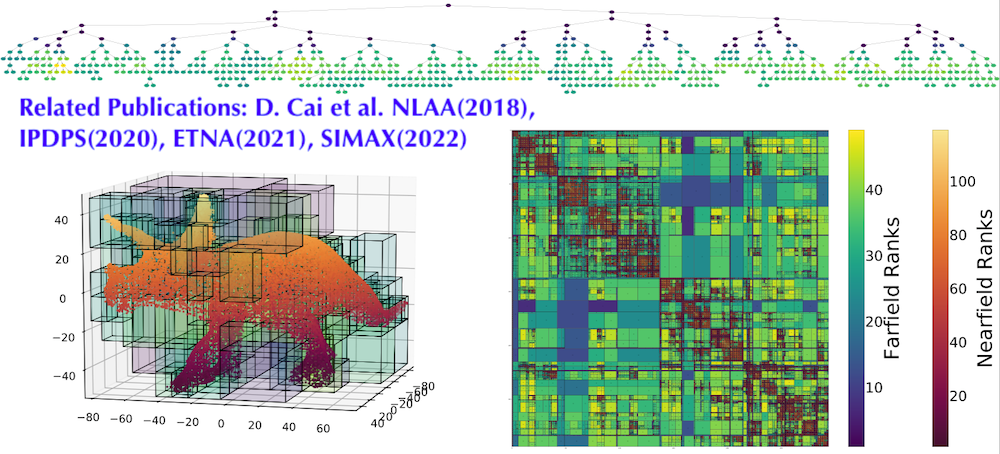
Hierarchical Data Compression
Modern machine and deep learning models rely on massive data and parameters to tackle challenging tasks,
which induce expensive memory use and training cost.
(1) How to reduce the computational complexity in face of massive data interactions?
(2) How to resolve the curse of dimensionality when inferencing with high dimensional data?
(3) Complex geometry? Numerical stability? Efficiency?
My recent work aims to develop novel data-driven techniques for constructing hierarchical representations to efficiently handle pairwise interactions, addressing the challenges brought by general interactions, complex geometry, and high dimensionality. The ultimate goal is to reduce the high complexity in time and space associated with SVM, kernel density estimation, Gaussian processes, transformer models, etc.
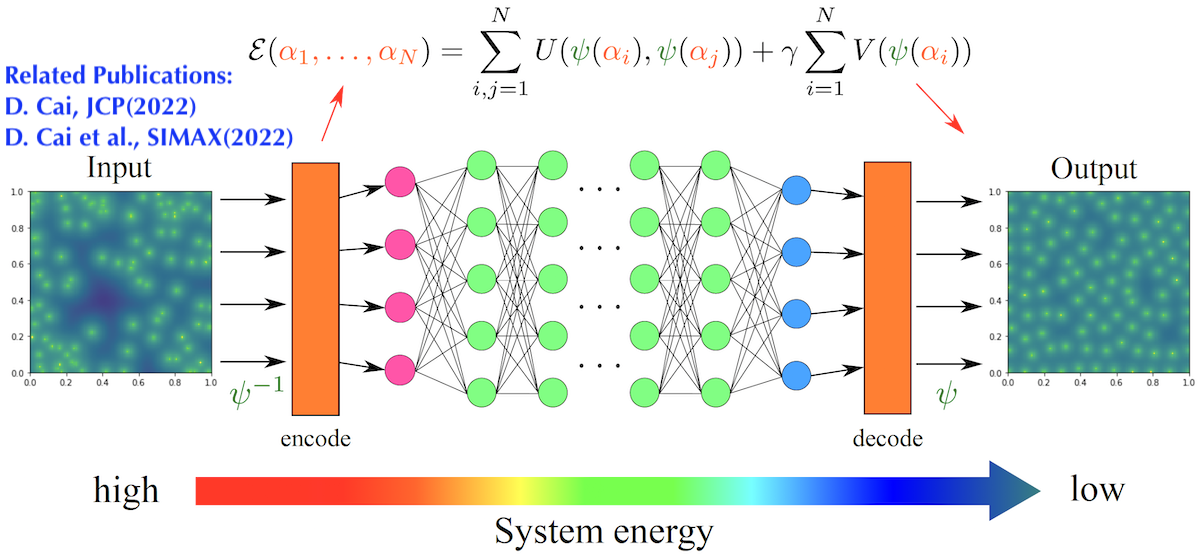
Physics-informed Distribution Learning
Generating data with a particular structure plays a key role in various applicatins such as variational inference, computer graphics, numerical integration, machine learning...
(1) How to improve a poor structure or distribution generated by an existing approach or an arbitrary approach?
(2) Number-theoretic approaches are limited to cubes, can we design a distribution transformer for general geometry?
(3) How to measure uniformity of points on a general geometry such as a manifold?
My recent work aims to develop a general and robust way to transform poor distributions. By integrating physics principles into the design of deep neural network, the new approach is able to achieve superior result and works for complex manifolds. The work has an impact on the efficient hierarchical data compression with possibly irregular data. Future work includes incorporating generative models such as normalizing flows for better efficiency and adjusting the approach for the efficient solution of PDEs using adaptive mesh generation.

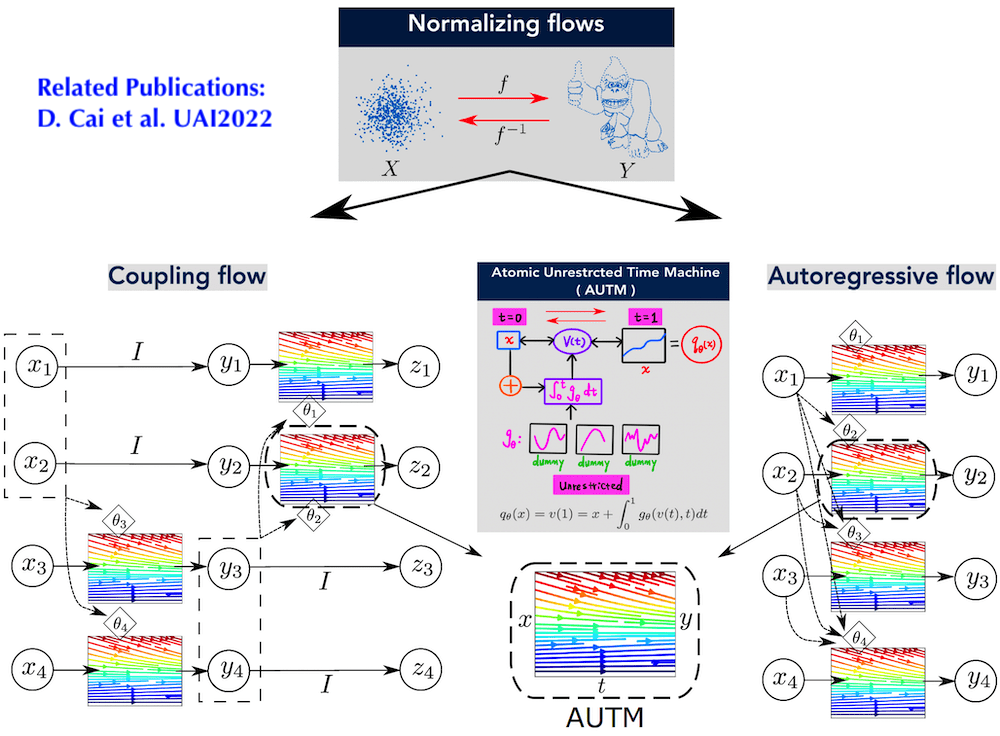
Density Estimation and Deep Generative Models
Normalizing flow is a powerful neural network architecture
that has been used in a wide range of applications such as variational inference, image generation, molecular dynamics, cosmological data analysis, etc.
It learns a bijective mapping from a latent base to the target distribution.
(1) How to design a normalizing flow with easy-to-compute inverse and log-likelihood?
(2) Can we guarantee the expressive power of the flow, i.e., universal approximation property?
(3) Can parameters be unrestricted for fast training without hindering invertibility?
My recent work investigates a versatile monotonic normalizing flow architecture with unrestricted parameters. The new architecture allows efficient inverse and log-likelihood computation and is rigorously shown to be a universal approximator for any monotonic normalizing flow. Experiments demonstrate overall better efficiency than state-of-the-art flow models. One interesting direction to study is to apply the model to adaptive mesh generation and distribution learning.
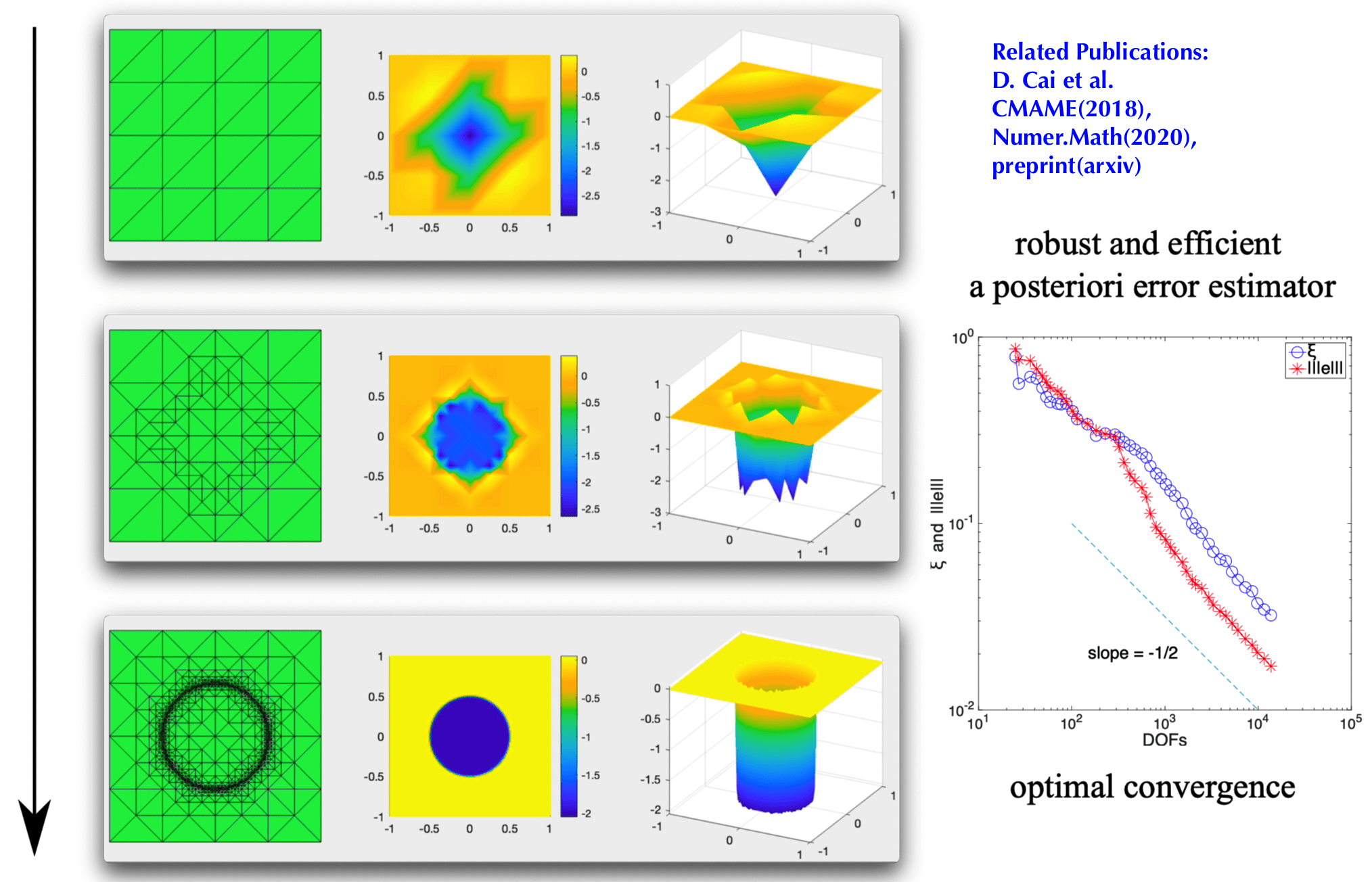
Adaptive Mesh Generation for PDEs w/ Nonsmooth Solutions
Partial Differential Equations (PDEs) with nonsmooth solutions are notoriously hard to solve numerically.
For challenging problems, naive discretizations can barely lead to any accuracy.
(1) How to estimate the error without knowing the true solution?
(2) How to achieve a desirable accuracy with minimal computational resource?
(3) Is it possible to generate a nearly optimal mesh without iterative refinement?
My past research concerns developing a posteriori error estimates that are robust to the singularity of the solution and are easy to compute. Inspired by my recent work in distribution learning and generative models, I become interested in using deep learning to "learn" the ideal mesh distribution without having to iteratively estimate the error and perform mesh refinement. The deep learning approach enables a general treatment of a wide class of PDEs and liberate users from sophisticated mathematical analysis that is often limited to certain class of PDEs.

Publications
- [ link ][ view ]
D. Cai, E. Chow, L. Erlandson, Y. Saad, and Y. Xi,
SMASH: Structured Matrix Approximation by Separation and Hierarchy
Numerical Linear Algebra with Applications 25 (6), e2204 (2018) - [ link ][ view ]
D. Cai, Z. Cai,
A Hybrid A Posteriori Error Estimator for Conforming Finite Element Approximations
Comput. Methods Appl. Mech. Eng. 339 (2018), 320-340 - [ link ][ view ]
D. Cai and P. S. Vassilevski,
Eigenvalue Problems for Exponential Type Kernels
Computational Methods in Applied Mathematics 20(1), 61-78 (2019) - [ link ][ view ]
D. Cai, Z. Cai, and S. Zhang,
Robust Equilibrated A Posteriori Error Estimator for Higher Order Finite Element Approximations to Diffusion Problems
Numerische Mathematik 144(1), 1-21(2020) - [ link ][ view ]
L. Erlandson, D. Cai, Y. Xi, and E. Chow,
Accelerating Parallel Hierarchical Matrix-Vector Products via Data-Driven Sampling
34th IEEE International Parallel and Distributed Processing Symposium (IPDPS), pp. 749-758, IEEE(2020) - [ link ][ view ]
D. Cai, J. Xia,
A Stable Matrix Version of The Fast Multipole Method: Stabilization Strategies and Examples
Electronic Transactions on Numerical Analysis 54, 581-609(2021) - [ link ][ view ]
D. Cai, Z. Cai
Hybrid A Posteriori Error Estimators for Conforming Finite Element Approximations to Stationary Convection-Diffusion-Reaction equations
preprint - [ link ][ view ]
D. Cai, J. Nagy, and Y. Xi
Fast Deterministic Approximation of Symmetric Indefinite Kernel Matrices with High Dimensional Datasets
SIAM Journal on Matrix Analysis and Applications 43 (2), 1003-1028(2022) - [ link ][ view ]
D. Cai, Y. Ji, H. He, Q. Ye, and Y. Xi
AUTM Flow: Atomic Unrestricted Time Machine for Monotonic Normalizing Flows
The 38th Conference on Uncertainty in Artificial Intelligence (UAI 2022) - [ link ][ view ]
D. Cai
Physics-informed Distribution Transformers via Molecular Dynamics and Deep Neural Networks
Journal of Computational Physics, 468:111511(2022) - [ link ][ view ]
D. Cai, E. Chow, Y. Xi
Data‐driven linear complexity low‐rank approximation of general kernel matrices: A geometric approach
Numerical Linear Algebra with Applications 30 (6), e2519 - [ link ][ view ]
D. Cai, H. Huang, E. Chow, Y. Xi
Data-driven construction of hierarchical matrices with nested bases
SIAM Journal on Scientific Computing, S24-S50 - [..][..] My research interests are spontaneous (to be revised)